题目内容
14. 已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,
已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
分析 ①分当a≥0时和当a<0时2种情况,分别根据f(a)=14,求得a的值.
②分当x≥0时和当x<0时2种情况,分别作出函数f(x)的图象.
解答 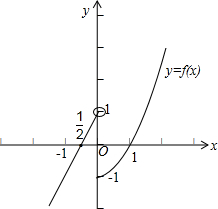 解:①∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,f(a)=14,
解:①∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,f(a)=14,
当a≥0时,由f(a)=2a-2=14,求得a=4;
当a<0时,由f(a)=1-2a=14,求得a=-$\frac{13}{2}$.
综上可得,a=4或a=-$\frac{13}{2}$.
②当x≥0时,把函数y=2x的图象向下平移2个单位,
可得f(x)的图象;
当x<0时,作出函数y=1-2x的图象即可得到f(x)的图象.
在平面直角坐标系中,作出函数y=f(x)的草图,如图所示:
点评 本题主要考查函数的图象的作法,函数的图象特征,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知{an}为等差数列,{bn}为正项等比数列,公比q≠1,若a1=b1,a13=b13,则( )
| A. | a7=b7 | B. | a7>b7 | C. | a7<b7 | D. | a7>b7或a7<b7 |
2.$\int_{\frac{π}{2}}^π{(sinx+cosx)}dx$的值是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | 2 | D. | 4 |
9.两直线x-2y+7=0和2x+y-1=0的交点坐标为( )
| A. | (1,3) | B. | (-1,3) | C. | (3,-1) | D. | (-3,-1) |