题目内容
4.已知数列{an}的前n项和为Sn,an=$\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n-1}+\sqrt{n+1})(\sqrt{n}+\sqrt{n+1})}$,则S2016=$\frac{1+12\sqrt{14}-\sqrt{2017}}{2}$.分析 将an=$\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n-1}+\sqrt{n+1})(\sqrt{n}+\sqrt{n+1})}$分子分母同乘$\sqrt{n+1}-\sqrt{n-1}$,再使用裂项法得出an=$\frac{1}{2}$($\frac{1}{\sqrt{n-1}+\sqrt{n}}$-$\frac{1}{\sqrt{n}+\sqrt{n+1}}$),从而得出S2016的值.
解答 解:an=$\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n-1}+\sqrt{n+1})(\sqrt{n}+\sqrt{n+1})}$=$\frac{\sqrt{n+1}-\sqrt{n-1}}{2(\sqrt{n-1}+\sqrt{n})(\sqrt{n}+\sqrt{n+1})}$
=$\frac{1}{2}$($\frac{1}{\sqrt{n-1}+\sqrt{n}}$-$\frac{1}{\sqrt{n}+\sqrt{n+1}}$).
∴S2016=$\frac{1}{2}$(1-$\frac{1}{1+\sqrt{2}}$)+$\frac{1}{2}$($\frac{1}{1+\sqrt{2}}$-$\frac{1}{\sqrt{2}+\sqrt{3}}$)+$\frac{1}{2}$($\frac{1}{\sqrt{2}+\sqrt{3}}$-$\frac{1}{\sqrt{3}+2}$)
+…+$\frac{1}{2}$($\frac{1}{\sqrt{2015}+\sqrt{2016}}$-$\frac{1}{\sqrt{2016}+\sqrt{2017}}$)
=$\frac{1}{2}$(1-$\frac{1}{1+\sqrt{2}}$+$\frac{1}{1+\sqrt{2}}$-$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$-$\frac{1}{\sqrt{3}+2}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$-$\frac{1}{\sqrt{2016}+\sqrt{2017}}$)
=$\frac{1}{2}$(1-$\frac{1}{\sqrt{2016}+\sqrt{2017}}$)
=$\frac{1}{2}$[1-($\sqrt{2017}-\sqrt{2016}$)]
=$\frac{1+\sqrt{2016}-\sqrt{2017}}{2}$
=$\frac{1+12\sqrt{14}-\sqrt{2017}}{2}$.
故答案为:$\frac{1+12\sqrt{14}-\sqrt{2017}}{2}$.
点评 本题考查了裂项法数列求和,寻找通项公式的分母特点进行裂项是关键,属于中档题.

 阅读快车系列答案
阅读快车系列答案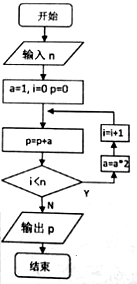 要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )| A. | 5 | B. | 6 | C. | 7 | D. | 4 |
| A. | y=($\sqrt{x}$)2 | B. | y=$\sqrt{{x}^{2}}$ | C. | y=$\left\{\begin{array}{l}{x,(x>0)}\\{-x,(x<0)}\end{array}\right.$ | D. | y=x |
 已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,
已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,