题目内容
3．
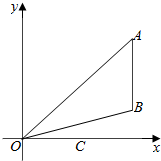已知O为坐标原点，向量$\overrightarrow{OA}$=（3cosx，3sinx），$\overrightarrow{OB}$=（3cosx，sinx），$\overrightarrow{OC}$=（$\sqrt{3}$，0），x∈（0，$\frac{π}{2}$）．（1）求证：（$\overrightarrow{OA}$-$\overrightarrow{OB}$）⊥$\overrightarrow{OC}$；
（2）若△ABC是等腰三角形，求x的值．
分析 （1）计算（$\overrightarrow{OA}-\overrightarrow{OB}$）$•\overrightarrow{OC}$=0即可；
（2）由AB=BC列出方程解出．
解答 解：（1）∵$\overrightarrow{OA}-\overrightarrow{OB}$=（0，2sinx），
∴$（\overrightarrow{OA}-\overrightarrow{OB}）•\overrightarrow{OC}=0×\sqrt{3}+2sinx×0=0$，
∴（$\overrightarrow{OA}$-$\overrightarrow{OB}$）⊥$\overrightarrow{OC}$．
（2）若△ABC是等腰三角形，则AB=BC，
∴（2sinx）2=（3cosx-$\sqrt{3}$）2+sin2x，整理得：$2{cos^2}x-\sqrt{3}cosx=0$，
解得cosx=0，或cosx=$\frac{\sqrt{3}}{2}$，
∵x∈（0，$\frac{π}{2}$），∴cosx=$\frac{\sqrt{3}}{2}$，x=$\frac{π}{6}$．
点评 本题考查了平面向量的数量积运算及模长计算，属于基础题．
练习册系列答案
相关题目
