题目内容
求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.
解:由 ∴l1,l2的交点为(1,2).
∴l1,l2的交点为(1,2).
设所求直线方程为y-2=k(x-1).
即kx-y+2-k=0,
∵P(0,4)到所求直线的距离为2,
∴2= ,解得k=0或k=
,解得k=0或k= .
.
∴直线方程为y=2或4x-3y+2=0.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如下:
| x | 3[ | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81[ | 89 | 90 | 91 |
已知: x
x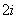 =280,
=280,
 y
y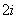 =45309,
=45309, xiyi=3487,此时r0.05=0.754.
xiyi=3487,此时r0.05=0.754.
(1)求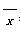 ,
,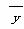 ;
;
(2)判断纯利润y与每天销售件数x之间是否线性相关.
 C.x+3y-7=0 D.3x+y-5=0
C.x+3y-7=0 D.3x+y-5=0 的直线l被圆x2+y2-2x-2y+1=0截得的弦长为
的直线l被圆x2+y2-2x-2y+1=0截得的弦长为 ,则直线l的斜率为__________.
,则直线l的斜率为__________. 直,l与C
直,l与C 交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )
交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )