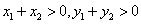题目内容
设等差数列{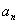 }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2,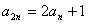 .
.
(1)求数列{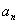 }的通项公式;
}的通项公式;
(2)设数列{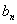 }满足
}满足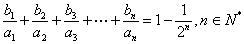 ,求{
,求{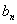 }的前n项和Tn;
}的前n项和Tn;
(3)是否存在实数K,使得Tn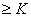 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由.

解得a1=1,d=2.
∴an=2n﹣1,n∈N*.(2)由已知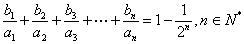 ,得:
,得:
当n=1时, ,
,
当n≥2时, ,显然,n=1时符合.
,显然,n=1时符合.
∴ ,n∈N*,由(1)知,an=2n﹣1,n∈N*.∴
,n∈N*,由(1)知,an=2n﹣1,n∈N*.∴ ,n∈N*.
,n∈N*.
又 ,∴
,∴ ,
,


练习册系列答案
相关题目
 的展开式中,含
的展开式中,含 项的系数等于 .(结果用数值作答)
项的系数等于 .(结果用数值作答) 中,
中, ,则数列
,则数列 的前5项和
的前5项和 =______.
=______.
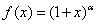 的定义域是
的定义域是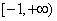 ,其中常数
,其中常数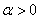 .
.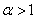 ,求
,求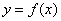 的过原点的切线方程.
的过原点的切线方程.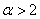 时,求最大实数
时,求最大实数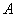 ,使不等式
,使不等式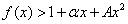 对
对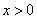 恒成立.
恒成立.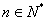 ,有
,有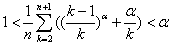 .
.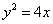 .
.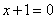 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;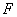 ,若过
,若过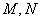 两点,若
两点,若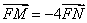 ,求直线
,求直线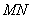 的斜率;
的斜率;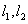 ,抛物线与
,抛物线与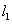 交于点
交于点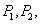 与
与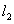 交于点
交于点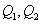 .
. 的图象大致是( )
的图象大致是( )
 同的概率;
同的概率;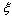 ,求
,求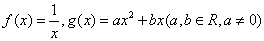 ,若
,若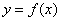 的图象与
的图象与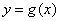 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点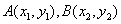 ,则下列判断正确的是
,则下列判断正确的是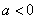 时,
时,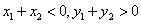 B. 当
B. 当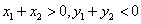
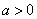 时,
时,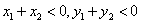 D. 当
D. 当