题目内容
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(Ⅰ)求甲、乙两人所付租车费相 同的概率;
同的概率;
(Ⅱ)设甲、乙两人所付租车费之和为随机变量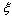 ,求
,求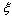 的分布列和数学期望E
的分布列和数学期望E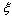

|
| 0 | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.37 | 0.28 | 0.13 | 0.02 |
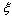 的数学期望
的数学期望 ,………………………11分
,………………………11分
答:甲、乙两人所付租车费相同的概率为0.37,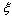 的数学期望E
的数学期望E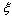 =1.4. …………12分
=1.4. …………12分
考点:1、互斥事件、独立事件、和事件;2、离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目
 满足
满足 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 等于( )
等于( )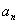 }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2,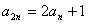 .
.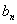 }满足
}满足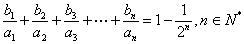 ,求{
,求{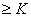 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由. 为实数,则下
为实数,则下 列命题正确的是( )
列命题正确的是( ) ,则
,则 B.若
B.若 ,则
,则
 D.若
D.若
 是不等式组
是不等式组 表示的平面区域
表示的平面区域 内的一动点,且不等式
内的一动点,且不等式 总成立,则
总成立,则 的取值范围是_________
的取值范围是_________ _______.
_______.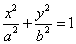 (a>b>0)经过点M(
(a>b>0)经过点M(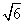 ,1),离心率为
,1),离心率为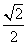 .
.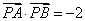 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由. 有( )
有( ) ,极小值
,极小值 B.极大值
B.极大值
 福”.
福”. 人,至少有2人为“幸福”的概率;
人,至少有2人为“幸福”的概率;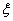 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求
 ,b=log
,b=log ,c=log
,c=log ,则()
,则()