题目内容
若等差数列{an}中前n项和为100,其后的2n项和为500,则紧随其后的3n项和为 .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:等差数列的每n项组合,组成一个新的数列,同样也是等差数列,只是新数列的增量是原数列增量的n倍,由此利用已知条件能求出结果.
解答:
解:等差数列的每n项组合,组成一个新的数列,
同样也是等差数列,只是新数列的增量是原数列增量的n倍,
设新数列的增量为x,则200+3x=500,
解得x=100,
则后面3n项的和为300+(3+4+5)x=1500.
故答案为:1500.
同样也是等差数列,只是新数列的增量是原数列增量的n倍,
设新数列的增量为x,则200+3x=500,
解得x=100,
则后面3n项的和为300+(3+4+5)x=1500.
故答案为:1500.
点评:本题考查等差数列的前n项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的灵活运用.

练习册系列答案
相关题目
已知集合A={-1,0,1},B={x|
<2x<4},则A∩B=( )
| 1 |
| 2 |
| A、{1} |
| B、{-1,1} |
| C、{0,1} |
| D、{-1,0,1} |
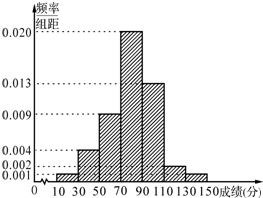 某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.










