Question

点P在平面ABC外,△ABC是等腰直角三角形,∠ABC=90°,△PAB是正三角形,PA⊥BC.

(1)求证:平面PAB⊥平面ABC;

(2)求二面角P-AC-B的大小.

Answer 1

(1)证明:∵BC⊥BA，BC⊥PA，

∴BC⊥平面PAB.又BC平面ABC，

∴平面PAB⊥平面ABC.

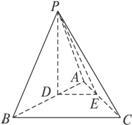
(2)解:取D为AB的中点，∵△PAB为正三角形，∴PD⊥AB.作DE⊥AC于E，连结PE.由（1）知平面PAB⊥平面ABC，

又PD⊥AB，∴PD⊥平面ABC.

∵DE⊥AC于E，∴AC⊥PE.

∴∠PED为二面角P-AC-B的平面角.

设AB=a，则PD=，AD=.

在Rt△ADE中，∠DAE=45°，

∴DE=.

在Rt△PDE中，tan∠PED=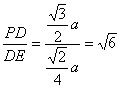，∴∠PED=arctan，

即二面角P-AC-B的大小为arctan.