题目内容
14.设a为实数,函数f(x)=x3-x2-x-a,若函数f(x)过点A(1,0),求函数在区间[-1,3]上的最值.分析 先求出a,得到函数的解析式,然后求解函数f(x)的导数,求出函数的单调区间,从而求出函数的最值.
解答 解:a为实数,函数f(x)=x3-x2-x-a,若函数f(x)过点A(1,0),
可得1-1-1-a=0,解得a=-1.
函数f(x)=x3-x2-x+1.
f′(x)=3x2-2x-1,
令f′(x)=0,则3x2-2x-1=0,
解得x1=-1,x2=$-\frac{1}{3}$.
列表如下:
| x | -1 | (-1,-$\frac{1}{3}$) | -$\frac{1}{3}$ | (-$\frac{1}{3}$,1) | 1 | (1,3) | 3 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | 0 | 递增 | $\frac{38}{27}$ | 递减 | 0 | 递增 | 16 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
19.已知定义域为[a-2,2a-1]的奇函数f(x)=x3-sinx+b+1,则f(a)+f(b)的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
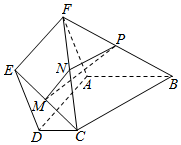 如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.
如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.