题目内容
2.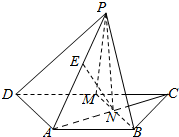 如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD(I)求证:AB⊥PN.
(Ⅱ)若E为PA的中点.求证:EN∥平面PDM.
分析 (1)连结AM,则可证△BCM为等边三角形,从而PN⊥BM,由面面垂直得出PN⊥平面ABMD,故而PN⊥AB;
(2)连结PC,由中位线定理得EN∥PC,故而EN∥平面PDM.
解答 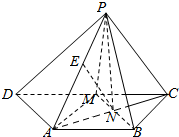 证明:(1)连结AM,
证明:(1)连结AM,
∵M是的CD的中点,AB=$\frac{1}{2}$CD,AB∥CD,
∴四边形ABCM是平行四边形,四边形ABMD是平行四边形,
∴N是BM的中点,BM=AD,又∵AD=BC,
∴△BCM是等边三角形,即△PBM是等边三角形.
∴PN⊥BM,∵平面PBM⊥平面ABMD,平面PBM∩平面ABMD=BM,PN?平面PBM,
∴PN⊥平面ABMD,∵AB?平面ABMD,
∴AB⊥PN.
(2)连结PC,∵E是PA的中点,N是AC的中点,
∴EN∥PC,
∵PC?平面PDM,EN?平面PDM,
∴EN∥平面PDM.
点评 本题考查了线面垂直的判断与性质,线面平行的判定,面面垂直的性质,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
12.椭圆C的焦点在x轴上,一个顶点坐标是(2,0),过焦点且垂直于长轴的弦长为1,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{14}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
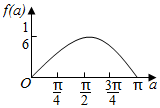
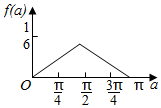
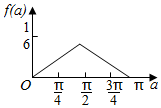
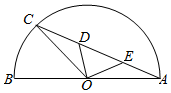 如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )
如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )