题目内容
11.已知p:x≥k,q:(x-1)(x+2)>0,若p是q的充分不必要条件,则实数k的取值范围是( )| A. | (-∞,-2) | B. | [-2,+∞) | C. | (1,+∞) | D. | [1,+∞) |
分析 利用不等式的解法、充分不必要条件的意义即可得出.
解答 解:q:(x-1)(x+2)>0,解得x>1或x<-2.
又p:x≥k,p是q的充分不必要条件,则实数k>1.
故选:C.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点为F(1,0),离心率为$\frac{{\sqrt{2}}}{2}$,过点F的动直线交M于A,B两点,若x轴上的点P(t,0)使得∠APO=∠BPO总成立(O为坐标原点),则t=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | -2 |
20.已知集合A={x|2x>1},B={x|x2-5x+6<0},则∁AB( )
| A. | (2,3) | B. | (-∞,2]∪[3,+∞) | C. | (0,2]∪[3,+∞) | D. | [3,+∞) |
1.函数$f(x)=cos(2x-\frac{2π}{3})+4{cos^2}x-2-\frac{3}{3x-π}(x∈[-\frac{11π}{12},\frac{19π}{12}])$所有零点之和为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
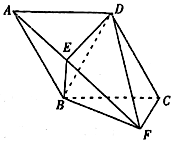 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.