题目内容
10.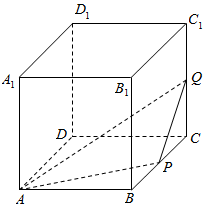 正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)
正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)①当x=0时,S为矩形,其面积最大为1;
②当x=y=$\frac{1}{2}$时,S为等腰梯形;
③当x=$\frac{1}{2}$,y=$\frac{3}{4}$时,S为六边形.
分析 根据题意,分别作出满足条件的图形,再根据空间中的线面位置关系找出对应的截面S,即可判断命题是否正确.
解答 解:对于①,当x=0时,截面S为矩形,且面积最大时为矩形ABC1D1,
最大面积为1×$\sqrt{2}$=$\sqrt{2}$,如图①所示,
∴①错误;
对于②,当x=y=$\frac{1}{2}$时,S为等腰梯形,如图②所示,
∴②正确;
对于③,当x=$\frac{1}{2}$,y=$\frac{3}{4}$时,
延长DD1至N,使D1N=$\frac{1}{2}$,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,
可得C1R=$\frac{1}{3}$,此时的截面形状仍然上图所示的APQRS,为五边形,
如图③所示
故③错误;
综上,正确的命题是②.
故答案为:②.
点评 本题以正方体为载体,考查了空间中的线面位置关系的应用问题,也考查了判断命题真假的应用问题,是中档题

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
19.在等比数列{an}中,a1=16,a6=2a5•a7,则a4=( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
20.已知α是三角形的最大内角,且cos2α=$\frac{1}{2}$,则$\frac{1-tanα}{1+tanα}$的值为( )
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 3-$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |
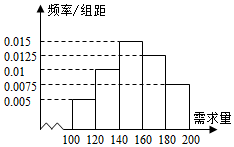 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.