曲线y=$\frac{1}{x}$与直线x=$\frac{1}{e}$.直线x=e及x轴所围成的封闭图形的面积等于2．题目和参考答案——青夏教育精英家教网—

题目内容

2．曲线y=$\frac{1}{x}$与直线x=$\frac{1}{e}$、直线x=e及x轴所围成的封闭图形的面积等于2．

分析由题意，利用定积分表示所围成的封闭图形的面积，利用定积分计算．

解答解：由题意，曲线y=$\frac{1}{x}$与直线x=$\frac{1}{e}$、直线x=e及x轴所围成的封闭图形的面积为${∫}_{\frac{1}{e}}^{e}\frac{1}{x}dx$=lnx|${\;}_{\frac{1}{e}}^{e}$=lne-ln$\frac{1}{e}$=2；
故答案为：2．

点评本题考查利用定积分求面积，解题的关键是确定被积区间及被积函数．

练习册系列答案

13．若以x轴正方向为始边，曲线上的点与圆心的连线为终边的角θ为参数，则圆x²+y²-2x=0的参数方程为$\left\{\begin{array}{l}{x=cosθ+1}\\{y=sinθ}\end{array}\right.$（θ为参数）．

10．

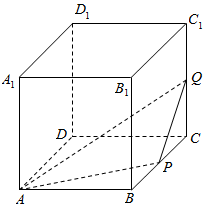正方体ABCD-A₁B₁C₁D₁的棱长为1，动点P，Q分别在棱BC，CC₁上，过点A，P，Q的平面截该正方体所得的截面记为S，设BP=x，CQ=y，其中x，y∈[0，1]，下列命题正确的是②．（写出所有正确命题的编号）
①当x=0时，S为矩形，其面积最大为1；
②当x=y=$\frac{1}{2}$时，S为等腰梯形；
③当x=$\frac{1}{2}$，y=$\frac{3}{4}$时，S为六边形．

17．

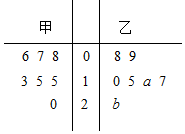甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示（下面简称甲数据、乙数据），且乙数据的众数为17，甲数据的平均数比乙数据平均数少2．
（1）求a，b的值．并计算乙数据的方差；
（2）现从甲、乙两组数据中随机各选一个数分别记为m，n．并进行对比分析，有放回的选取2次，记m＞n的次数为X．求X的数学期望E（X）．

7．

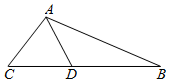如图，在△ABC中，∠BAC=120°，AB=2，AC=1，D是BC边上的一点（包括端点），若$\overrightarrow{AD}$•$\overrightarrow{BC}$∈[m，n]，则$\frac{n}{m-n}$的值为$-\frac{2}{7}$．

14．若a=$\int_{-\frac{π}{2}}^{\frac{π}{2}}$（$\frac{1}{π}$-sinx）dx，则（x-$\frac{a}{{\sqrt{x}}}$）⁶的二项展开式中的常数项为15（用数字作答）．

11．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的是（　　）

12．已知（x-y）（x+y）⁵的展开式中x²y⁴的系数为m，则${∫}_{1}^{2}$（x^m+$\frac{1}{x}$）dx=ln2+$\frac{15}{64}$．

试题分类