题目内容
已知函数 .
.
(Ⅰ)若 ,求函数
,求函数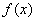 的单调区间和极值;
的单调区间和极值;
(Ⅱ)设函数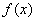 图象上任意一点的切线
图象上任意一点的切线 的斜率为
的斜率为 ,当
,当 的最小值为1时,求此时切线
的最小值为1时,求此时切线 的方程.
的方程.
解:(I) 的定义域为(
的定义域为( )时,
)时,
当 时,
时,
由 得
得 ,
,
由 得
得 ,或
,或 ,由
,由 得
得 ,
,
∴ 的单调递增区间为
的单调递增区间为 ,
, ;单调递减区间为
;单调递减区间为
∴ 极大值为
极大值为 ;极小值为
;极小值为
(II)由题意知 ∴
∴
此时 ,即
,即 ,∴
,∴ ,切点为
,切点为 ,
,
∴此时的切线 方程为:
方程为: .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
某小卖部销售一品牌饮料的零售价 (元/瓶)与销量
(元/瓶)与销量 (瓶)的关系统计如下:
(瓶)的关系统计如下:
| 零售价 |
|
|
|
|
|
|
| 销量 | 50 | 44 | 43 | 40 | 35 | 28 |
已知 的关系符合线性回归方程
的关系符合线性回归方程 ,其中
,其中 ,
, .当单价为
.当单价为 元时,估计该小卖部销售这种品牌饮料的销量为
元时,估计该小卖部销售这种品牌饮料的销量为
A.  B.
B. C.
C. D.
D.
 )-sin2(x-
)-sin2(x-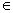 (
( ,
, )的值域是_______。
)的值域是_______。 ,则圆锥侧面积等于___________.
,则圆锥侧面积等于___________.





 ,则
,则 .
.
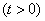 .
.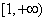 上为增函数,求实数
上为增函数,求实数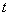 的取值范围;
的取值范围;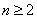 且
且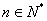 时,证明:
时,证明: 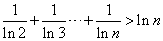 .
.  B.
B. C.
C. D.
D.

 的准线方程是
的准线方程是 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
