题目内容
已知函数
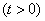 .
.
(Ⅰ)若函数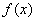 在
在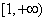 上为增函数,求实数
上为增函数,求实数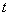 的取值范围;
的取值范围;
(Ⅱ)当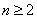 且
且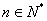 时,证明:
时,证明: 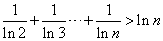 .
.
解:(I)函数 的定义域为
的定义域为 .
.
 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,
上恒成立,
. ∵ ∴
∴ ,∴
,∴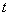 的取值范围为
的取值范围为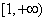
(Ⅱ)由(I)当 ,
, 时,
时, ,又
,又 ,
,
∴ (当
(当 时,等号成立),即
时,等号成立),即 又当
又当 时,设
时,设 ,
,
则 ∴
∴ 在
在 上递减,
上递减,
∴ ,即
,即 在
在 恒成立,
恒成立,
∴ 时,
时, …①恒成立,(当且仅当
…①恒成立,(当且仅当 时,等号成立),
时,等号成立),
用 代替
代替 ,
,  …②恒成立(当且仅当
…②恒成立(当且仅当 时,等号成立),
时,等号成立),
∴当 时,
时, ,由①得
,由①得 ,即
,即 ,
,
当 时,
时, ,
, ,由②得
,由②得 .
.
∴当 时,
时, ,即
,即 .
.
∴ ,
,  ,
,  ,
,

 .
.
∴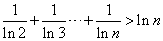 .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
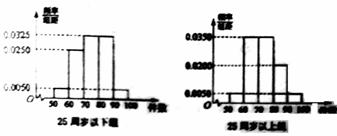
 的解的个数为( )
的解的个数为( ) ,且
,且 ,则当
,则当 时,
时, 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 .
. ,求函数
,求函数 的斜率为
的斜率为 ,当
,当 B.
B. C.
C. D.
D.

 中,
中, ,
, ,则
,则 .
. ,函数
,函数 在
在 单调递减,则
单调递减,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
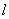 是一条直线,
是一条直线,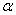 ,
,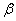 ,
,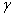 是不同的平面,则下列说法不正确的是
是不同的平面,则下列说法不正确的是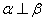 ,那么
,那么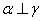 ,
,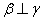 ,
,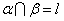 ,那么
,那么