Question

5．设定义在R上的函数f（x）=$\left\{\begin{array}{l}{\frac{1}{|x-3|}，x≠3}\\{1，x=3}\end{array}\right.$，若关于x的方程f²（x）+af（x）+b=0有5个不同实数解，则实数a的取值范围是a＜-1且a≠-2．

Answer 1

分析 作函数f（x）=$\left\{\begin{array}{l}{\frac{1}{|x-3|}，x≠3}\\{1，x=3}\end{array}\right.$的图象，从而利用数形结合知x²+ax+b=0有2个不同的正实数解，且其中一个为1，从而可得-1-a＞0且-1-a≠1；从而解得．

解答 解：作函数f（x）=$\left\{\begin{array}{l}{\frac{1}{|x-3|}，x≠3}\\{1，x=3}\end{array}\right.$的图象如下，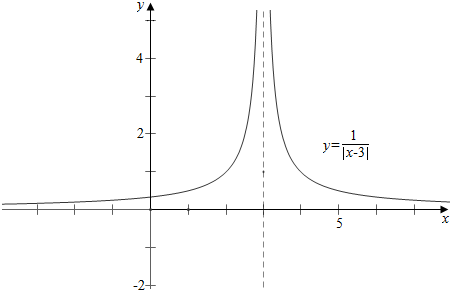
，
∵关于x的方程f²（x）+af（x）+b=0有5个不同实数解，
∴x²+ax+b=0有2个不同的正实数解，且其中一个为1；
故1+a+b=0，故b=-a-1，
故x²+ax+b=x²+ax-1-a=（x-1）（x+1+a）=0，
故-1-a＞0且-1-a≠1；
故a＜-1且a≠-2；
故答案为：a＜-1且a≠-2．

点评 本题考查了数形结合的思想应用及分段函数的应用，同时考查了因式分解的应用．