题目内容
已知函数f(x)＝a－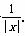
.
(1)求证：函数y＝f(x)在(0，＋∞)上是增函数；
(2)若f(x)<2x在(1，＋∞)上恒成立，求实数a的取值范围．
解：(1)证明：当x∈(0，＋∞)时， f(x)＝a－
，
设0<x1<x2，则x1x2>0，x2－x1>0.
f(x1)－f(x2)＝
＝
<0.
∴f(x1)<f(x2)，即f(x)在(0，＋∞)上是增函数．
(2)由题意a－<2x在(1，＋∞)上恒成立，设h(x)＝2x＋，则a<h(x)在(1，＋∞)上恒成立．
可证h(x)在(1，＋∞)上单调递增．
故a≤h(1)，即a≤3，
∴a的取值范围为(－∞，3]．
练习册系列答案
相关题目
，求A∪B.
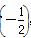，b＝f(2)，c＝f(3)，则a，b，c的大小关系为( )
＝( )
，若函数f(x)是奇函数，则g(－4)＝________.