题目内容
在平面直角坐标系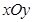 中,已知点
中,已知点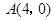 ,动点
,动点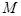 在
在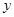 轴上的正射影为点
轴上的正射影为点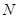 ,且满足直线
,且满足直线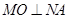 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)当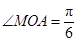 时,求直线
时,求直线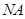 的方程.
的方程.
 中,已知点
中,已知点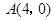 ,动点
,动点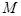 在
在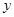 轴上的正射影为点
轴上的正射影为点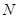 ,且满足直线
,且满足直线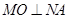 .
.(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)当
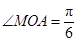 时,求直线
时,求直线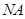 的方程.
的方程.(Ⅰ) (
( );(Ⅱ)
);(Ⅱ) 或
或
 (
( );(Ⅱ)
);(Ⅱ) 或
或
试题分析:(Ⅰ)属直接法求轨迹问题,再根据
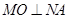 列式子时,可根据直线垂直斜率相乘等于
列式子时,可根据直线垂直斜率相乘等于 列出方程,但需注意斜率存在与否的问题,还可转化为向量垂直问题,用数量积为0列出方程(因此法不用讨论故常选此法解决直线垂直问题)。因点
列出方程,但需注意斜率存在与否的问题,还可转化为向量垂直问题,用数量积为0列出方程(因此法不用讨论故常选此法解决直线垂直问题)。因点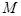 不能与原点重合故
不能与原点重合故 。(Ⅱ)
。(Ⅱ) 即直线
即直线 的倾斜角为
的倾斜角为 或
或 。故可求出直线
。故可求出直线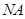 的斜率,由点斜式可求直线
的斜率,由点斜式可求直线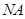 的方程。
的方程。试题解析:解:(Ⅰ)设
 ,则
,则 ,
, ,
, . 2分
. 2分因为 直线
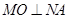 ,
,所以
 ,即
,即 . 4分
. 4分所以 动点
 的轨迹C的方程为
的轨迹C的方程为 (
( ). 5分
). 5分(Ⅱ)当
 时,因为
时,因为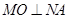 ,所以
,所以 .
.所以 直线
 的倾斜角为
的倾斜角为 或
或 .
.当直线
 的倾斜角为
的倾斜角为 时,直线
时,直线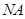 的方程为
的方程为 ; 8分
; 8分当直线
 的倾斜角为
的倾斜角为 时,直线
时,直线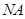 的方程为
的方程为 . 10分
. 10分
练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
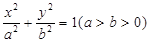 上的点
上的点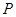 到左右两焦点
到左右两焦点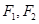 的距离之和为
的距离之和为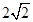 ,离心率为
,离心率为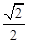 .
.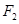 的直线
的直线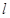 交椭圆于
交椭圆于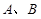 两点,若
两点,若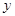 轴上一点
轴上一点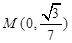 满足
满足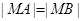 ,求直线
,求直线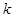 的值.
的值.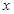 轴的抛物线经过点
轴的抛物线经过点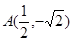 .
.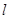 过定点
过定点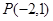 ,斜率为
,斜率为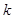 ,当
,当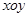 中,已知
中,已知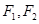 分别是椭圆
分别是椭圆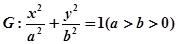 的左、右焦点,椭圆
的左、右焦点,椭圆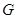 与抛物线
与抛物线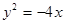 有一个公共的焦点,且过点
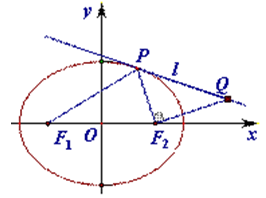
有一个公共的焦点,且过点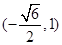 .
.
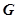 的方程;
的方程;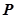 是椭圆
是椭圆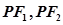 ,过
,过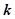 的直线
的直线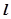 ,使得
,使得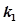 ,
,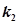 ,试证明
,试证明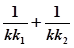 为定值,并求出这个定值;
为定值,并求出这个定值;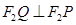 ,设
,设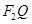 交
交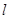 于点
于点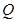 ,
,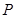 在椭圆上移动时,点
在椭圆上移动时,点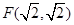 及直线
及直线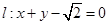 ,曲线
,曲线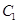 是满足下列两个条件的动点
是满足下列两个条件的动点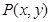 的轨迹:①
的轨迹:①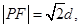 其中
其中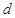 是
是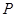 到直线
到直线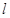 的距离;②
的距离;②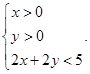
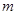 与曲线
与曲线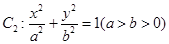 均相切于同一点,求椭圆
均相切于同一点,求椭圆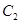 离心率
离心率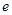 的取值范围.
的取值范围.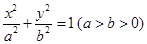 的左、右顶点分别为
的左、右顶点分别为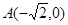 、
、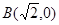 ,离心率
,离心率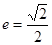 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且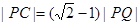 .
.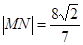 ,求直线MN的方程.
,求直线MN的方程.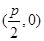 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.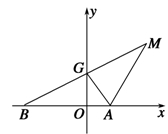
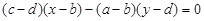 与曲线
与曲线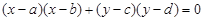 的交点个数是 .
的交点个数是 .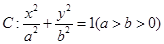 的左顶点
的左顶点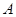 的斜率为
的斜率为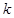 的直线交椭圆于另一个点
的直线交椭圆于另一个点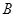 ,且点
,且点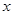 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点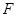 ,若
,若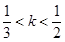 ,则椭圆离心率的取值范围是_____________.
,则椭圆离心率的取值范围是_____________.