题目内容
若椭圆
+
=1的离心率为e=
,则实数m的值等于 .
| x2 |
| 5 |
| y2 |
| m |
| ||
| 2 |
考点:椭圆的简单性质
专题:高考数学专题,圆锥曲线的定义、性质与方程
分析:首先要判断哪个是a,哪个是b,因此需要分类讨论,再根据离心率联立解得即可.
解答:
解:由椭圆
+
=1
当m<5时,a=
,c=
=
,
∴e=
=
=
解得,m=
,
当m>5时,a=
,c=
=
∴e=
=
=
解得,m=10,
故答案为:
或10
| x2 |
| 5 |
| y2 |
| m |
当m<5时,a=
| 5 |
| a2-b2 |
| 5-m |
∴e=
| c |
| a |
| ||
|
| ||
| 2 |
解得,m=
| 5 |
| 2 |
当m>5时,a=
| m |
| a2-b2 |
| m-5 |
∴e=
| c |
| a |
| ||
|
| ||
| 2 |
解得,m=10,
故答案为:
| 5 |
| 2 |
点评:本题主要考查了椭圆的简单性质,以及离心率的计算公式,考查了分类讨论的思想,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
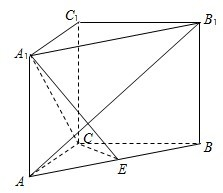 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.