题目内容
7.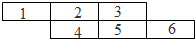 用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
分析 由题意可分三类,根据分类计数原理可得.
解答 解:从6个区域人选5个区域有(1,2,3,4,5),(1,2,3,4,6),(1,2,3,5,6),(1,2,4,5,6),(1,3,4,5,6),(2,3,4,5,6),共6种,
若(1,2,3,4,5),(2,3,4,5,6)各涂一色,则剩下的一个区域有4种涂法,共有A55A41=480种,
若(1,2,3,5,6),(1,2,4,5,6),(1,3,4,5,6),各涂一色,则剩下的一个区域有3种涂法,共有A55A31=360种,
若(1,2,3,4,6)各涂一色,则剩下的一个区域有2种涂法,共有A55A21=240种,
故共有480+360+240=1080种,
故答案为:1080.
点评 本题考查了分类计数原理,关键是分类,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
17.对于非零向量$\overrightarrow a,\overrightarrow b$,“$2\overrightarrow a+3\overrightarrow b=\overrightarrow 0$”是“$\overrightarrow{a}$∥$\overrightarrow b$”成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
2.已知an=$\frac{n-\sqrt{2008}}{n-\sqrt{2009}}$,且数列{an}中共有100项,则此数列中最小项和最大项分别为第( )项.
| A. | 42,43 | B. | 43,44 | C. | 44,45 | D. | 45,46 |
16.已知函数f(x)=(x-$\frac{1}{x}$)•sinx,x∈[-π,π]且x≠0,下列描述正确的是( )
| A. | 函数f(x)为奇函数 | B. | 函数f(x)既无最大值也无最小值 | ||
| C. | 函数f(x)有4个零点 | D. | 函数f(x)在(0,π)单调递增 |