题目内容
18.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象过点M($\frac{3π}{4}$,0),且在区间[0,$\frac{π}{2}$]上是单调函数.求ω和φ的值及相应的函数解析式.分析 根据函数f(x)是偶函数求出φ的值,再根据函数过点($\frac{3π}{4}$,0)求出ω的值,即得f(x)的解析式.
解答 解:∵函数f(x)=sin(ωx+φ)是R上的偶函数,且0≤φ≤π,
∴φ=$\frac{π}{2}$;
又sin(ω•$\frac{3π}{4}$+$\frac{π}{2}$)=0,ω>0,f(x)=sin(ωx+φ)在区间[0,$\frac{π}{2}$]上是单调函数,
∴ω•$\frac{3π}{4}$+$\frac{π}{2}$=2π,解得ω=2;
∴f(x)=sin(2x+$\frac{π}{2}$).
点评 本题主要考查利用y=Asin(ωx+φ )的图象特征求解析式的应用问题,是基础题目.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
9.已知曲线C:x2+y2+xy+m=0,经过点(1,-1),则m=( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
3.已知△ABC的三个内角A,B,C的对边依次为a,b,c,满足$\frac{tanB}{tanC}$=$\frac{b}{2a-b}$.
(1)求角C的大小;
(2)若c=2,求△ABC周长的取值范围.
(1)求角C的大小;
(2)若c=2,求△ABC周长的取值范围.
8.sin4$\frac{π}{12}$-cos4$\frac{π}{12}$等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
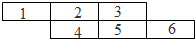 用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.