题目内容
15.已知数列{an}的前n项和为Sn,Sn=$\frac{1}{3}$(an-1)(n∈N,n≥1).(1)求a1,a2;
(2)求数列{an}的通项公式;
(3)bn=n,令cn=bnan,求数列{cn}的前n项和.
分析 (1)通过令n=1、2代入计算即得结论;
(2)通过Sn=$\frac{1}{3}$(an-1)(n∈N,n≥1)与Sn-1=$\frac{1}{3}$(an-1-1)(n∈N,n≥2)作差,计算可知数列{an}是首项、公比均为-$\frac{1}{2}$的等比数列,进而计算可得结论;
(3)通过(2)可知cn=n•$(-\frac{1}{2})^{n}$,进而利用错位相减法计算即得结论.
解答 解:(1)依题意,a1=S1=$\frac{1}{3}$(a1-1),
解得:a1=-$\frac{1}{2}$,
当n=2时,a2-$\frac{1}{2}$=S2=$\frac{1}{3}$(a2-1),
解得:a2=$\frac{1}{4}$;
(2)∵Sn=$\frac{1}{3}$(an-1)(n∈N,n≥1),
∴Sn-1=$\frac{1}{3}$(an-1-1)(n∈N,n≥2),
两式相减得:an=$\frac{1}{3}$(an-an-1),即an=-$\frac{1}{2}$an-1,
又∵a1=-$\frac{1}{2}$,
∴数列{an}是首项、公比均为-$\frac{1}{2}$的等比数列,
∴其通项公式an=(-1)n$\frac{1}{{2}^{n}}$;
(3)由(2)可知cn=bnan=n•$(-\frac{1}{2})^{n}$,记数列{cn}的前n项和为Tn,
则Tn=$-\frac{1}{2}$+2•$(-\frac{1}{2})^{2}$+3•$(-\frac{1}{2})^{3}$+…+n•$(-\frac{1}{2})^{n}$,
-$\frac{1}{2}$Tn=$(-\frac{1}{2})^{2}$+2•$(-\frac{1}{2})^{3}$+3•$(-\frac{1}{2})^{4}$+…+(n-1)•$(-\frac{1}{2})^{n}$+n•$(-\frac{1}{2})^{n+1}$,
两式相减得:$\frac{3}{2}$Tn=$-\frac{1}{2}$+$(-\frac{1}{2})^{2}$+$(-\frac{1}{2})^{3}$+…+$(-\frac{1}{2})^{n}$-n•$(-\frac{1}{2})^{n+1}$
=$\frac{-\frac{1}{2}[1-(-\frac{1}{2})^{n}]}{1+\frac{1}{2}}$-n•$(-\frac{1}{2})^{n+1}$
=-$\frac{1}{3}$+$\frac{2+3n}{6}$•$(-\frac{1}{2})^{n}$,
∴Tn=-$\frac{2}{9}$+$\frac{2+3n}{9}$•$(-\frac{1}{2})^{n}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | y=x2•sinx | B. | y=x•cosx | C. | y=ln|x| | D. | y=2x-1 |
(1)求角C的大小;
(2)若c=2,求△ABC周长的取值范围.
| A. | x2=2y | B. | x2=$\sqrt{2}$y | C. | x2=y | D. | x2=$\frac{\sqrt{2}}{2}y$ |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
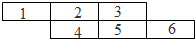 用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.