题目内容
12.在△ABC中,a、b、c分别为角A、B、C所对的边,已知tan(A+B)=-$\sqrt{3}$,c=$\frac{7}{2}$,又△ABC面积S=$\frac{3\sqrt{3}}{2}$,则(1)△ABC的周长是否为一定值?若是,请求出该定值;若不是,请说明理由.
(2)△ABC是否能够唯一确定?若能,请解出此三角形;若不能,请适当修改条件以确定△ABC.
分析 (1)利用诱导公式可得tanC=$\sqrt{3}$,由C∈(0,π),可得C=$\frac{π}{3}$,由S=$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,解得ab=6,由余弦定理可得:a+b=$\frac{11}{2}$,从而可求△ABC的周长=9.
(2)由(1)可得ab=6,a+b=$\frac{11}{2}$,可得:2b2-11b+12=0,解得:b=4或$\frac{3}{2}$,a=$\frac{3}{2}$或4,△ABC不能够唯一确定,修改条件为:在△ABC中,a、b、c分别为角A、B、C所对的边,已知tan(A+B)=-$\sqrt{3}$,c=$\frac{7}{2}$,又△ABC面积S=$\frac{121\sqrt{3}}{64}$,△ABC能够唯一确定.
解答 解:(1)△ABC的周长为一定值.
∵tan(A+B)=-tanC=-$\sqrt{3}$,
∴tanC=$\sqrt{3}$,由C∈(0,π),可得:C=$\frac{π}{3}$,
又∵c=$\frac{7}{2}$,△ABC面积S=$\frac{1}{2}$absinC=$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,解得:ab=6,
∴由余弦定理c2=a2+b2-2abcosC,可得:$\frac{49}{4}$=a2+b2-ab=(a+b)2-3ab=(a+b)2-18,可得:a+b=$\frac{11}{2}$,
∴△ABC的周长=a+b+c=$\frac{7}{2}$+$\frac{11}{2}$=9,故△ABC的周长为一定值9.
(2)由(1)可得C=$\frac{π}{3}$,c=$\frac{7}{2}$,ab=6,a+b=$\frac{11}{2}$,可得:2b2-11b+12=0,解得:b=4或$\frac{3}{2}$,a=$\frac{3}{2}$或4.
故△ABC不能够唯一确定,
修改条件为:在△ABC中,a、b、c分别为角A、B、C所对的边,已知tan(A+B)=-$\sqrt{3}$,c=$\frac{7}{2}$,又△ABC面积S=$\frac{121\sqrt{3}}{64}$,
可得:$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=$\frac{121\sqrt{3}}{64}$,解得:ab=$\frac{121}{16}$,又a+b=$\frac{11}{2}$,
从而解得:b2-$\frac{11}{2}$b+$\frac{121}{16}$=0,△=0,可得b,a只有唯一解.
点评 本题主要考查了诱导公式,三角形面积公式,余弦定理,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于中档题.

(1)求角C的大小;
(2)若c=2,求△ABC周长的取值范围.
| A. | x2=2y | B. | x2=$\sqrt{2}$y | C. | x2=y | D. | x2=$\frac{\sqrt{2}}{2}y$ |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
| A. | 2a | B. | 4a | C. | a | D. | $\frac{1}{2}$a |
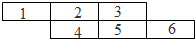 用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.