题目内容
20.已知x<0,y<0,且3x+y=-2,则xy的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 由题意和基本不等式列出关于xy不等式,化简后求出xy的最大值.
解答 解:∵x<0,y<0,且3x+y=-2,
∴-x>0,-y>0,-3x+(-y)=2,
∴2=-3x+(-y)≥2$\sqrt{(-3x)(-y)}$=$2\sqrt{3xy}$,
则$xy≤\frac{1}{3}$,当且仅当-3x=-y时取等号,
即xy的最大值是$\frac{1}{3}$,
故选C.
点评 本题考查了基本不等式,注意使用的条件:一正二定三相等,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.投资者王先生第一天以5元/股的价格买进100股某股票,第2天该股票的价格涨了5%,但王先生认为它还会继续涨,就没有售出,到了第3天,该股票下跌了4%,王先生担心它继续下跌,把股票全部卖出了.如果不计交易的手续费和 税费,那么通过这次交易,王先生一共获利( )
| A. | 5元 | B. | 4元 | C. | 1元 | D. | 4.5元 |
8.下列命题中正确的是( )
| A. | 若?服从正态分布N(1,2),且P(?>2)=0.1,则P(0<?<2)=0.2 | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
5.已知数列{an}前n项和满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$ (n≥2),a1=1,则an=( )
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
12.将一骰子抛掷两次,所得向上点数分别为m和n,则函数y=x2-2(2m-n)x+1在[6,+∞)上为增函数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
9.$\sqrt{si{n}^{2}480°}$等于( )
| A. | ±$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
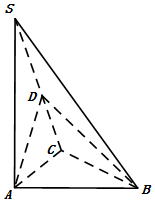 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC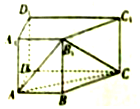 如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.
如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.