题目内容
14.若点(2,1)是抛物线y2=2px(p>0)的一条弦的中点,且这条弦所在的直线的斜率为1,则p的值是1.分析 利用点差法,结合直线的斜率,即可求出p的值.
解答 解:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
两式相减,得(y1-y2)(y1+y2)=2p(x1-x2),
依题意x1≠x2,∴kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=1,
于是y1+y2=2p=2,
因此p=1.
故答案为:1.
点评 本题考查直线与抛物线的位置关系,考查点差法的运用,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点P($\frac{1}{2}$,m)是抛物线C上一点,若点P到直线l的距离等于点P到坐标原点O的距离,则点F到准线l的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知等差数列{an}中,a1+a4=11,a2=4,则a3的值是( )
| A. | 9 | B. | 8 | C. | 7 | D. | 2 |
19.已知变量x,y之间具有线性相关关系,其散点图如图所示,则其回归方程可能为( )
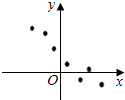

| A. | $\widehat{y}$=1.5x+2 | B. | $\widehat{y}$=-1.5x+2 | C. | $\widehat{y}$=1.5x-2 | D. | $\widehat{y}$=-1.5x-2 |
3.工人月工资y(元)与劳动生产率x(千元)变化的回归直线方程为$\widehat{y}$=50+80x,下列判断不正确的是( )
| A. | 劳动生产率为1000元时,工资约为130元 | |
| B. | 工人月工资与劳动者生产率具有正相关关系 | |
| C. | 劳动生产率提高1000元时,则工资约提高130元 | |
| D. | 当月工资为210元时,劳动生产率约为2000元 |