题目内容
4.某型号汽车在某种路面的刹车距离s(米)与汽车车速x(千米/时)的关系式是s=$\frac{1}{60}$x2.若该车在行驶过程中发现前面40米处有障碍物,这时为了能在距离障碍物不少于5米处停车,问最大限制时速应是多少?(假定汽车发现障碍物到刹车经过1.5秒钟)分析 设最大限制时速为x千米/时.汽车在离开障碍物40-5=35(米)处,必须停下,建立方程,即可得出结论.
解答 解:设最大限制时速为x千米/时,汽车在离开障碍物40-5=35(米)处,必须停下.
另外,1.5秒钟内,汽车行驶的距离是:1.5×$\frac{1}{3600}$×x×1000=$\frac{5}{12}$x(米),
因此,$\frac{5}{12}$x+=$\frac{1}{60}$x2=35,
所以x2+25x-35×60=0,
所以(x+60)(x-35)=0,于是得到x=35,
即最大限制时速为35千米/时.
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,注意单位的统一.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
19.若x∈C,则关于x的方程x2-5|x|+6=0的所有解的和为( )
| A. | 0 | B. | 5 | C. | 10 | D. | 5i |
14.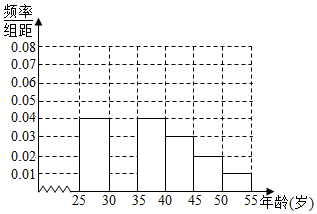 某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:
某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:
(Ⅰ)补全频率分布直方图并求n、a、p的值;
(Ⅱ)从[40,50)岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动,其中选取2人作为领队,求选取的2名领队年龄都在[40,45)岁的概率.
 某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:
某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 已养成垃圾分类习惯的人数 | 占本组频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六祖 | [50,55] | 15 | 0.3 |
(Ⅱ)从[40,50)岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动,其中选取2人作为领队,求选取的2名领队年龄都在[40,45)岁的概率.
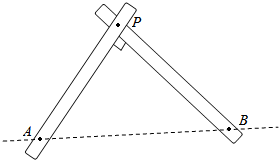 如图所示,两根杆分别绕着点A和B(AB=2a)在平面内转动,并且转动时两杆保持互相垂直,求杆的交点P的轨迹方程.
如图所示,两根杆分别绕着点A和B(AB=2a)在平面内转动,并且转动时两杆保持互相垂直,求杆的交点P的轨迹方程.