题目内容
16．求函数y=sin2x+4sinx-3的值域．分析 利用换元法，转化为二次函数在指定区间上的值域问题，注意变量的范围的变化．
解答 解：令t=sinx，则-1≤t≤1
y=t2+4t-3=（t+2）2-7，函数的对称轴为：t=-2．
∴函数在[-1，-1]上单调增，∴t=-1时，函数取得最小值为-6，t=1时，函数确定最大值2．
∴函数y=sin2x+4sinx-3的值域为[-6，2]
故答案为：[-6，2]．
点评 本题考查三角函数的值域，解题的关键是利用换元法，转化为二次函数在指定区间上的值域问题．
练习册系列答案
同步奥数系列答案
相关题目
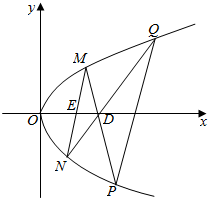如图，在平面直角坐标系中，已知抛物线C：y2=2px（p＞0）．设点D（n，0），E（m，0）．M为抛物线C上的动点（异于顶点），连接ME并延长交抛物线C于点N，连接MD、ND并延长交抛物线C于点P、Q，连接PQ．设直线MN、PQ的斜率存在且分别为k1，k2．