题目内容
学校选派6位学生前往德国A、B、C、D、E、F六所不同的学校交流学习,每所学校安排1名学生,假设每位学生被安排到各学校的可能性相同,则学生甲没被安排到B校且学生已被安排到C校的概率为 .
考点:相互独立事件的概率乘法公式
专题:计算题,概率与统计
分析:求出学校选派6位学生前往德国A、B、C、D、E、F六所不同的学校交流学习,每所学校安排1名学生,共有
=720种,学生甲没被安排到B校且学生已被安排到C校,共有
=96种,利用古典概型概率公式可求.
| A | 6 6 |
| C | 1 4 |
| A | 4 4 |
解答:
解:学校选派6位学生前往德国A、B、C、D、E、F六所不同的学校交流学习,每所学校安排1名学生,共有
=720种,学生甲没被安排到B校且学生已被安排到C校,共有
=96种,
∴学生甲没被安排到B校且学生已被安排到C校的概率为
=
.
故答案为:
| A | 6 6 |
| C | 1 4 |
| A | 4 4 |
∴学生甲没被安排到B校且学生已被安排到C校的概率为
| 96 |
| 720 |
| 2 |
| 15 |
故答案为:
| 2 |
| 15 |
点评:本题考查概率的计算,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
某班班会准备从含甲、乙的7人中选取4人发言,要求甲、乙两人至少有一人参加,且若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A、720种 | B、520种 |
| C、600种 | D、360种 |
已知抛物线C:y2=x与直线l:y=kx+1,“k<0”是“直线l与抛物线C有两个不同交点”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知α=
,则点P(sinα,tanα)所在的象限是( )
| 5π |
| 8 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
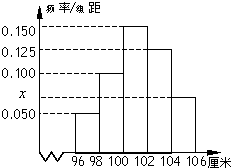 某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].