题目内容
13.[A]已知函数f(x)=alnx+$\frac{1-a}{2}{x}^{2}-x$,0<a<1.(1)讨论函数f(x)的单调性;
(2)关于x的不等式f(x)<$\frac{a}{a-1}$在[1,+∞)上有解,求实数a的取值范围.
分析 (1)f′(x)=$\frac{a}{x}$+(1-a)x-1=$\frac{(1-a)(x-\frac{a}{1-a})(x-1)}{x}$(x>0).(0<a<1).对a分类讨论:①当a=$\frac{1}{2}$时;②$0<a<\frac{1}{2}$时,$0<\frac{a}{1-a}<1$;③$\frac{1}{2}<a<1$时,$\frac{a}{1-a}>1$.利用导数研究其单调性即可得出单调区间.
(2)关于x的不等式f(x)<$\frac{a}{a-1}$在[1,+∞)上有解,可得f(x)min<$\frac{a}{a-1}$.由(1)利用单调性即可得出最小值,解出不等式即可.
解答 解:(1)f′(x)=$\frac{a}{x}$+(1-a)x-1=$\frac{(1-a)(x-\frac{a}{1-a})(x-1)}{x}$(x>0).(0<a<1).
①当a=$\frac{1}{2}$时,f′(x)=$\frac{(x-1)^{2}}{2x}$≥0,因此函数f(x)在(0,+∞)上单调递增;
②$0<a<\frac{1}{2}$时,$0<\frac{a}{1-a}<1$,函数f(x)在$(0,\frac{a}{1-a})$,(1,+∞)上单调递增;在$(\frac{a}{1-a},1)$上单调递减.
③$\frac{1}{2}<a<1$时,$\frac{a}{1-a}>1$,函数f(x)在(0,1),($\frac{a}{1-a}$,+∞)上单调递增;在$(1,\frac{a}{1-a})$上单调递减.
(2)关于x的不等式f(x)<$\frac{a}{a-1}$在[1,+∞)上有解,∴f(x)min<$\frac{a}{a-1}$.
由(1)可得:$0<a≤\frac{1}{2}$时,函数f(x)在[1,+∞)上单调递增,∴x=1时,f(x)取得最小值,f(1)=-$\frac{1+a}{2}$.
∴-$\frac{1+a}{2}$$<\frac{a}{a-1}$,解得$0<a<\sqrt{2}-1$.
$\frac{1}{2}<a<1$时,函数f(x)在($\frac{a}{1-a}$,+∞)上单调递增;在$(1,\frac{a}{1-a})$上单调递减.
∴f(x)min=$f(\frac{a}{1-a})$=$aln\frac{a}{1-a}$+$\frac{{a}^{2}-2a}{2(1-a)}$<$\frac{a}{a-1}$.化为:$ln\frac{a}{1-a}$+$\frac{a}{2(1-a)}$<0,
令$\frac{a}{1-a}$=t,∵$\frac{1}{2}<a<1$,∴t>1,g(t)=lnt+$\frac{1}{2}t$>ln1+$\frac{1}{2}$=$\frac{1}{2}>$0,因此$ln\frac{a}{1-a}$+$\frac{a}{2(1-a)}$<0无解.
综上可得:实数a的求值范围是$(0,\sqrt{2}-1)$.
点评 本题考查了利用导数研究函数的单调性极值与最值、解不等式,考查了分类讨论方法、推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | x1<-2 | B. | x2>0 | C. | x3<1 | D. | x3>2 |
| A. | $\frac{8π}{3}$ | B. | $\frac{32π}{3}$ | C. | 8π | D. | $\frac{8\sqrt{2}π}{3}$ |
| x | -2 | 0 | 1 | 3 | 8 |
| f′(x) | -10 | 6 | 8 | 0 | -90 |
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)求f(x)的单调区间.
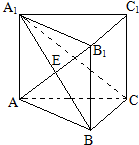 已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,
已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,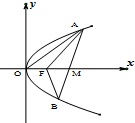 已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.
已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.