题目内容
10.设有抛物线C:y=-x2+$\frac{9}{2}$x-4,过原点O作C的切线y=kx,使切点P在第一象限,求切线方程.分析 设出切点坐标,求出切线方程,联立方程组,利用判别式为0,求解即可.
解答 解:设点P的坐标为(x1,y1),则y1=kx1①
y1=-x${\;}_{1}^{2}$+$\frac{9}{2}$x1-4②
①代入②得x${\;}_{1}^{2}$+(k-$\frac{9}{2}$)x1+4=0.
∵P为切点,
∴△=(k-$\frac{9}{2}$)2-16=0得k=$\frac{17}{2}$或k=$\frac{1}{2}$…(6分)
当k=$\frac{17}{2}$时,x1=-2,y1=-17.
当k=$\frac{1}{2}$时,x1=2,y1=1.
∵P在第一象限,
∴所求的斜率k=$\frac{1}{2}$.
故所求切线方程为y=$\frac{1}{2}$x…(10分)
点评 本题考查直线与抛物线的位置关系的应用,切线方程的求法,考查计算能力.

练习册系列答案
相关题目
1.若集合{a,b,c,d}={1,2,3,4},且下列四个关系:①a=1;②b≠1;③c=2;④d≠4有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是 ( )
| A. | 1种 | B. | 6种 | C. | 8种 | D. | 9种 |
18.已知点P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1上一点,若PF1⊥PF2,则△PF1F2的面积为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
5.已知复数z=a2+(b-2)i的实部和虚部分别是2和3,则实数a,b的值分别是( )
| A. | $\sqrt{2}$,1 | B. | $\sqrt{2}$,5 | C. | ±$\sqrt{2}$,5 | D. | ±$\sqrt{2}$,1 |
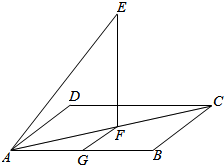 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题:
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题: