题目内容
3.已知函数f(x)=x2-2lnx(Ⅰ) 求函数f(x)的单调递减区间;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)>x(x+a)恒成立,求实数a的取值范围.
分析 (Ⅰ)求函数的定义域和导数,利用函数单调性和导数之间的关系进行求解即可.
(Ⅱ)利用参数分离法进行参数分离,构造函数,求函数的导数,了利用导数研究函数的最值即可.
解答 解:(?)函数f(x)的定义域为(0,+∞),
${f^/}(x)=2x-\frac{2}{x}=\frac{2(x+1)(x-1)}{x}$
当x∈(0,1)时,f′(x)<0,
函数f(x)的单调递减区间为(0,1)
(Ⅱ)由f(x)>x(x+a)得x2-2lnx>x(x+a),
∴ax<-2lnx,
∴$a<-\frac{2lnx}{x}$
记$g(x)=-\frac{2lnx}{x}$,
则${g^/}(x)=-\frac{2-2lnx}{x^2}$,
令g′(x)=0得x=e
当x∈(0,e)时,g′(x)<0;
当x∈(e,+∞)时,g′(x)>0
∴g(x)的最小值为$g(e)=-\frac{2}{e}$,
于是$a<-\frac{2}{e}$
所以实数a的取值范围是$(-∞,-\frac{2}{e})$.
点评 本题主要考查函数单调性的判断,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
12.图1是某学生的数学考试成绩的茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14,图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图,那么程序框图输出的结果是( )
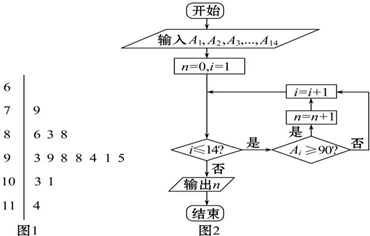

| A. | 14 | B. | 9 | C. | 10 | D. | 7 |
8.已知x,y∈R+,且满足x+2y=2xy,那么x+4y的最小值为( )
| A. | 3-$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
15.若函数f(x)=$\left\{\begin{array}{l}{ax+a,x≤0}\\{xlnx,x>0}\end{array}\right.$ 的图象上有且仅有两对点关于原点对称,则a的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{e}$)∪(1,e) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |