题目内容
2.已知函数f(x)=2sin(2x+$\frac{π}{6}$),则f(x)的单调递增区间是[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.分析 令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,求出x的范围,可得函数f(x)的单调递增区间.
解答 解:函数f(x)=2sin(2x+$\frac{π}{6}$),
令 2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,
解得2kπ-$\frac{2π}{3}$≤2x≤2kπ+$\frac{π}{3}$,k∈Z,
即kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z;
所以函数f(x)的单调递增区间是[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
故答案为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
点评 本题主要考查了正弦函数的单调性问题,是基础题.

练习册系列答案
相关题目
12.正四棱柱ABCD-A1B1C1D1中,底面边长为2,侧棱长为4,则B1点到平面AD1C的距离为( )
| A. | $\frac{8}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{4}{3}$ |
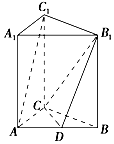 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.