题目内容
5. 如图,在长方体ABCD-A1B1C1D1中,点E在棱CC1的延长线上,且CC1=C1E=BC=$\frac{1}{2}$AB=1.
如图,在长方体ABCD-A1B1C1D1中,点E在棱CC1的延长线上,且CC1=C1E=BC=$\frac{1}{2}$AB=1.(1)求D1E的中点F到平面ACB1的距离;
(2)求证:平面D1B1E⊥平面DCB1.
分析 (1)连接AD1、BC1,可得四边形AB1ED1是平行四边形,即D1E∥平面ACB1,可得点F到平面ACB1的距离等于点E到平面ACB1的距离,由${V_{E-AC{B_1}}}={V_{A-{B_1}CE}}$,得D1E的中点F到平面ACB1的距离.
(2)由已知得,${B_1}{C^2}+{B_1}{E^2}=4=C{E^2}$,则B1E⊥B1C,CD⊥B1E,即B1E⊥平面DCB1,又B1E?平面D1B1E,即可得平面D1B1E⊥平面DCB1.
解答  证明:(1)连接AD1、BC1,∵$A{D_1}\underline{\underline{∥}}B{C_1}\underline{\underline{∥}}{B_1}E$,
证明:(1)连接AD1、BC1,∵$A{D_1}\underline{\underline{∥}}B{C_1}\underline{\underline{∥}}{B_1}E$,
∴四边形AB1ED1是平行四边形,
∴D1E∥AB1,又AB1?平面AB1C,D1E?平面AB1C,
∴D1E∥平面ACB1,
∴点F到平面ACB1的距离等于点E到平面ACB1的距离,由${V_{E-AC{B_1}}}={V_{A-{B_1}CE}}$,
得$\frac{1}{3}{S_{△AC{B_1}}}•h=\frac{1}{3}×\frac{1}{2}×1×2×2$,又易知${S_{△AC{B_1}}}=\frac{3}{2}$.
∴D1E的中点F到平面ACB1的距离为$h=\frac{4}{3}$.
(2)由已知得,${B_1}{C^2}+{B_1}{E^2}=4=C{E^2}$,则B1E⊥B1C,
由长方体的特征可知CD⊥平面B1BCE,
而B1E?平面B1BCE,所以CD⊥B1E,
∴B1E⊥平面DCB1,又B1E?平面D1B1E,
∴平面D1B1E⊥平面DCB1.
点评 本题考查了空间线面、面面位置关系,点面距离,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知i为虚数单位,复数z满足z(1+i)=1,则z的共轭复数$\overline{z}$=( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{2}-\frac{1}{2}i$ | C. | $-\frac{1}{2}+\frac{1}{2}i$ | D. | $-\frac{1}{2}-\frac{1}{2}i$ |
10.集合A={x|x(2-x)>0},B={x|x-1≥0},则集合A∪B=( )
| A. | {x|1≤x<2} | B. | {x|x>2} | C. | {x|x≥1或x<0} | D. | {x|x>0} |
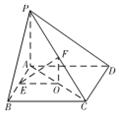 如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.
如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.