题目内容
口袋中装有大小质地都相同、编号为1,2,3,4,5,6的球各一只.现从中一次性随机地取出两个球,设取出的两球中较小的编号为X,则随机变量X的数学期望是 .
考点:离散型随机变量的期望与方差
专题:计算题,概率与统计
分析:确定X的可能取值为1,2,3,4,5,求出相应的概率,可求随机变量X的数学期望
解答:
解:由题设知X的可能取值为1,2,3,4,5.
随机地取出两个球,共有:
=15种,
∴P(X=1)=
,P(X=2)=
,P(X=3)=
,P(X=4)=
,P(X=5)=
,
∴随机变量X的分布列为
故EX=1×
+2×
+3×
+4×
+5×
=
.
故答案为:
.
随机地取出两个球,共有:
| C | 2 6 |
∴P(X=1)=
| 5 |
| 15 |
| 4 |
| 15 |
| 3 |
| 15 |
| 2 |
| 15 |
| 1 |
| 15 |
∴随机变量X的分布列为
| X | 1 | 2 | 3 | 4 | 5 | ||||||||||
| P |
|
|
|
|
|
| 5 |
| 15 |
| 4 |
| 15 |
| 3 |
| 15 |
| 2 |
| 15 |
| 1 |
| 15 |
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:本题考查离散型随机变量的数学期望的求法,确定X的可能取值,求出相应的概率是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
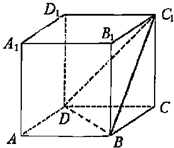 已知ABCD-A1B1C1D1是棱长为1的正方体.
已知ABCD-A1B1C1D1是棱长为1的正方体.