��Ŀ����
5��������y=x2+$\frac{1}{{x}^{2}+a}��a��0��$����Сֵʱ��ijͬѧ���������£��ɻ�������ʽ��y=x2+$\frac{1}{{x}^{2}+a}={x}^{2}+a+\frac{1}{{x}^{2}+a}-a��2\sqrt{��{x}^{2}+a��\frac{1}{{x}^{2}+a}}$-a=2-a����˺���y=x2+$\frac{1}{{x}^{2}+a}$����СֵΪ2-a��
����ͬѧ�Ľⷨ��ȷ����a��ȡֵ��Χ�ǣ�0��1]��
���� �ɲ���ʽ����ֵ�Ⱥų������������a��ȡֵ��Χ��
��� �⣺��a��0��
��y=x2+$\frac{1}{{x}^{2}+a}={x}^{2}+a+\frac{1}{{x}^{2}+a}-a��2\sqrt{��{x}^{2}+a��\frac{1}{{x}^{2}+a}}$-a=2-a��
���ҽ���${x}^{2}+a=\frac{1}{{x}^{2}+a}$��ʵ����ʱ��ʽ�Ⱥų�����
��x2+a=1��ʵ���⣬��x2=1-a��ʵ���⣬
��1-a��0����a��1��
��a��0��
��a��ȡֵ��Χ�ǣ�0��1]��
�ʴ�Ϊ����0��1]��
���� ���⿼���������ʽ��ѵ�������û�������ʽ����ֵ�÷������ؼ�����ȷ���û�������ʽ����ֵ�����������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
17���߳�Ϊ2��������ABCD�Ķ��㶼��ͬһ�����ϣ����ĵ�ƽ��ABCD�ľ���Ϊ1�������ı����Ϊ��������
| A�� | 3�� | B�� | 5�� | C�� | 12�� | D�� | 20�� |
14����֪����f��x���Ƕ�����R�ϵ�ż�������ҵ�x��0ʱ��f��x��=log3��x+1������f��a2-1����1����ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | ��-$\sqrt{3}$��$\sqrt{3}$�� | B�� | ��-1��1�� | C�� | ��-�ޣ�-$\sqrt{3}$���ȣ�$\sqrt{3}$��+�ޣ� | D�� | ��-�ޣ�-1���ȣ�1��+�ޣ� |
15������f��x��=f�䣨x����ʵ����x0��������f��x���ġ���פ�㡱���������g��x��=lnx�ġ���פ�㡱Ϊ������ô�����㣨������
| A�� | ��=1 | B�� | 0������1 | C�� | 2������3 | D�� | 1������2 |
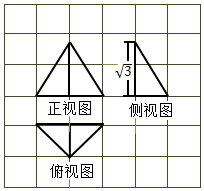 ����ֽ�ĸ�С���DZ߳�Ϊ1�������Σ�ͼ�д�ʵ��������һ�������������ͼ����������ͼ���������Σ���ü���������������Ϊ$\frac{16��}{3}$��
����ֽ�ĸ�С���DZ߳�Ϊ1�������Σ�ͼ�д�ʵ��������һ�������������ͼ����������ͼ���������Σ���ü���������������Ϊ$\frac{16��}{3}$��