题目内容
若定义在R上的函数f(x)满足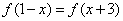 ,且
,且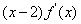 <0a="f" (
<0a="f" (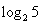 ),b="f" (
),b="f" (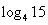 ),c="f" (
),c="f" (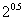 ),则a,b,c的大小关系为
),则a,b,c的大小关系为
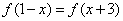 ,且
,且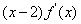 <0a="f" (
<0a="f" (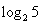 ),b="f" (
),b="f" (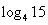 ),c="f" (
),c="f" (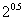 ),则a,b,c的大小关系为
),则a,b,c的大小关系为| A.a>b>c | B.c>b>a | C.b>a>c | D.c>a>b |
C
试题分析:
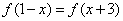
 对称轴为
对称轴为 ,
, 中当
中当 时
时 ,函数
,函数 递增,当
递增,当 时
时 ,函数
,函数 递减,
递减,
 结合单调性可知
结合单调性可知
点评:比较函数值大小,借助于函数单调性转化为比较自变量的大小

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 .
. 的单调性;
的单调性;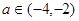 及
及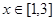 时,恒有
时,恒有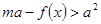 成立,求实数
成立,求实数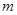 的取值范围.
的取值范围.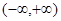 上的单调性,并用定义证明.
上的单调性,并用定义证明.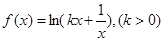 在
在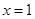 处取得极小值.
处取得极小值.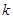 的值;
的值;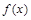 在
在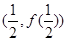 处的切线方程为
处的切线方程为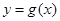 ,求证:当
,求证:当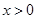 时,曲线
时,曲线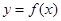 不可能在直线
不可能在直线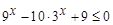 ,求函数
,求函数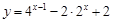 的最大值和最小值;
的最大值和最小值;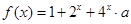 在
在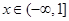 上f (x)
上f (x)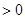 恒成立,求a的取值范围.
恒成立,求a的取值范围.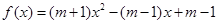
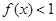 的解集为
的解集为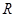 ,求
,求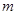 的取值范围;
的取值范围;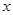 的不等式
的不等式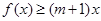 ;
;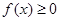 对一切
对一切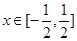 恒成立,求
恒成立,求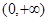 的函数
的函数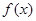 ,对任意的
,对任意的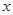 、
、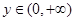 ,都有
,都有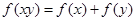 ,且当
,且当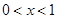 时,
时,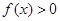 .
.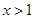 时,
时,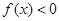 ;
;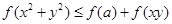 恒成立,求实数
恒成立,求实数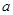 的取值范围.
的取值范围.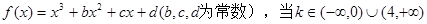 时,
时,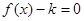 只有一个实根;当
只有一个实根;当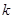 ∈(0,4)时,
∈(0,4)时,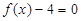 和
和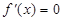 有一个相同的实根;
有一个相同的实根;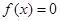 和
和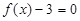 的任一实根大于
的任一实根大于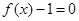 的任一实根;
的任一实根; 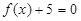 的任一实根小于
的任一实根小于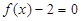 的任一实根.
的任一实根. ,则
,则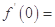 .
.