题目内容
已知函数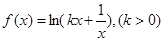 在
在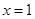 处取得极小值.
处取得极小值.
(1)求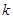 的值;
的值;
(2)若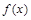 在
在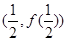 处的切线方程为
处的切线方程为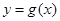 ,求证:当
,求证:当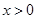 时,曲线
时,曲线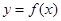 不可能在直线
不可能在直线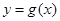 的下方.
的下方.
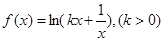 在
在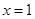 处取得极小值.
处取得极小值.(1)求
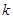 的值;
的值;(2)若
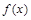 在
在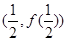 处的切线方程为
处的切线方程为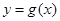 ,求证:当
,求证:当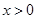 时,曲线
时,曲线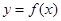 不可能在直线
不可能在直线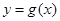 的下方.
的下方.(1) (2)证明当
(2)证明当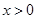 时,曲线
时,曲线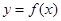 不可能在直线
不可能在直线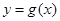 的下方.那么只要证明存在一个变量函数值大于函数
的下方.那么只要证明存在一个变量函数值大于函数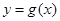 的函数值,即可。
的函数值,即可。
 (2)证明当
(2)证明当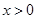 时,曲线
时,曲线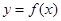 不可能在直线
不可能在直线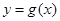 的下方.那么只要证明存在一个变量函数值大于函数
的下方.那么只要证明存在一个变量函数值大于函数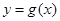 的函数值,即可。
的函数值,即可。试题分析:解:(1)
 ,由已知得
,由已知得 3分
3分当
 时
时 ,此时
,此时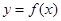 在
在 单调递减,在
单调递减,在 单调递增 5分
单调递增 5分A.
 ,
, ,
,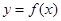 在
在 的切线方程为
的切线方程为 ,即
,即 8分
8分当
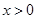 时,曲线
时,曲线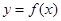 不可能在直线
不可能在直线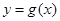 的下方
的下方
 在
在 恒成立,令
恒成立,令 ,
,
当
 ,
, ,即
,即
 在
在 恒成立,所以当
恒成立,所以当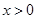 时,曲线
时,曲线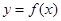 不可能在直线
不可能在直线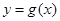 的下方 13分
的下方 13分点评:主要是考查了导数的运用,研究函数的单调性,以及函数的最值,属于中档题。

练习册系列答案
相关题目
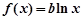 ,
,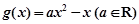
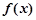 与
与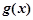 在公共点
在公共点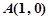 处有相同的切线,求实数
处有相同的切线,求实数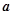 、
、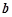 的值;
的值;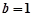 时,若曲线
时,若曲线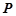 处有相同的切线,求证:点
处有相同的切线,求证:点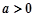 ,
,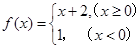 ,则
,则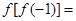 ( )
( )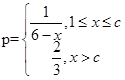 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.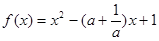 ,
,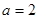 时,解不等式
时,解不等式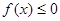 ;
;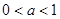 ,解关于
,解关于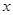 的不等式
的不等式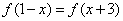 ,且
,且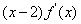 <0a="f" (
<0a="f" (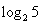 ),b="f" (
),b="f" (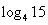 ),c="f" (
),c="f" (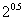 ),则a,b,c的大小关系为
),则a,b,c的大小关系为 为全集,
为全集, ,则
,则 ( )
( )



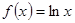 ,
,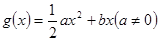
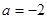 时,
时,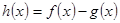 在其定义域内单调递增,求
在其定义域内单调递增,求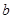 的取值范围;
的取值范围;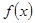 的图象
的图象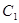 与函数
与函数 的图象
的图象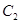 交于
交于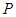 ,
,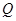 两点,过线段
两点,过线段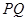 的中点
的中点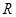 作
作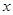 轴的垂线分别交
轴的垂线分别交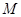 ,
,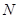 ,问是否存在点
,问是否存在点 分)已知函数
分)已知函数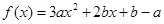 (
(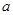 ,
,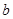 是不同时为零的常数).
是不同时为零的常数).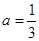 时,若不等式
时,若不等式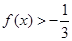 对任意
对任意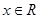 恒成立,求实数
恒成立,求实数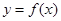 在
在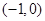 内至少存在一个零点.
内至少存在一个零点.