题目内容
15.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,($\overrightarrow{a}$-2$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 据题意可设$|\overrightarrow{a}|=|\overrightarrow{b}|=m$,并且m≠0,进行数量积的运算,由$(\overrightarrow{a}-2\overrightarrow{b})•\overrightarrow{a}=0$便可求出$cos<\overrightarrow{a},\overrightarrow{b}>$的值,进而得出$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:设$|\overrightarrow{a}|=|\overrightarrow{b}|=m$,则:
$(\overrightarrow{a}-2\overrightarrow{b})•\overrightarrow{a}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}$=${m}^{2}-2{m}^{2}cos<\overrightarrow{a},\overrightarrow{b}>$=0;
∵m≠0;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故选B.
点评 考查向量数量积的运算及计算公式,向量夹角的范围,已知三角函数值求角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如图所示是某几何体的三视图,则该几何体的体积是( )


| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
10.已知集合A={x|x-1<0},B={x∈N|x<4},则(∁RA)∩B=( )
| A. | {0} | B. | {1,2,3} | C. | {1} | D. | {1,2} |
20.如果函数f(x)=3sin(2x+ϕ)的图象关于直线$x=\frac{2}{3}π$对称,那么|φ|的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.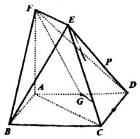 如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.
如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.