题目内容
7. 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.(Ⅰ)求证:AE⊥平面PCD;
(Ⅱ)求二面角B-PA-C的余弦值;
(Ⅲ)在棱PB上是否存在点M,使得CM∥平面AEF?若存在,求$\frac{PM}{PB}$的值;若不存在,说明理由.
分析 (Ⅰ)推导出PD=AD,从而△PAD是等边三角形,进而AE⊥PD,再求出CD⊥AB,从而CD⊥平面PAB,进而CD⊥AE,由此能证明AE⊥平面PCD.
(Ⅱ)以A为原点,作Ax∥DC,以AB所在直线为y轴,建立空间直角坐标系,利用向量法能求出二面角B-PA-C的余弦值.
(Ⅲ)在平面ABP中,延长AE交BP为G,取BG中点M,推导出G为PM中点,此时,$\frac{PM}{PB}$=$\frac{2}{3}$从而DM∥平面AEF,推导出面CDM∥面AEF,从而得到CM∥面AEF.
解答 证明:(Ⅰ)∵AP⊥BP,D是AB中点,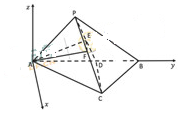
∴PD=AD,
又∠PAB=60°,∴△PAD是等边三角形,
又E为PD的中点,∴AE⊥PD,
∵AC⊥BC,∠ABC=45°,
又D是AB的中点,∴CD⊥AB,
∵平面PAB⊥平面ABC,又平面PAB∩平面ABC=AB,
∴CD⊥平面PAB,∵AE?平面PAB,∴CD⊥AE,
又CD∩PD=D,∴AE⊥平面PCD.
解:(Ⅱ)以A为原点,作Ax∥DC,以AB所在直线为y轴,建立空间直角坐标系,
设AB=2a,则A(0,0,0),B(0,2a,0),C(a,a,0),D(0,a,0),P(0,$\frac{a}{2},\frac{\sqrt{3}a}{2}$),
∵CD⊥平面PAB,∴平面PAB的一个法向量为$\overrightarrow{CD}$=(-a,0,0),
设平面PAC的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{AP}•\overrightarrow{n}=\frac{a}{2}y+\frac{\sqrt{3}}{2}az=0}\\{\overrightarrow{AC}•\overrightarrow{n}=ax+ay=0}\end{array}\right.$,令x=1,得$\overrightarrow{n}$=(1,-1,$\frac{\sqrt{3}}{3}$),
设二面角B-PA-C的平面角为θ,
由图知,二面角B-PA-C为锐角,
∴cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{CD}|}{|\overrightarrow{n}|•|\overrightarrow{CD}|}$=$\frac{a}{\sqrt{\frac{7}{3}}a}$=$\frac{\sqrt{21}}{7}$,
∴二面角B-PA-C的余弦值为$\frac{\sqrt{21}}{7}$.
(Ⅲ)PB上存在M,使得CM∥平面AEF,此时$\frac{PM}{PB}=\frac{2}{3}$.
证明:在平面ABP中,延长AE交BP为G,
取BG中点M,∵M为BG中点,D为AB中点,
∴DM∥AG,又E为PD中点,∴G为PM中点,
此时,$\frac{PM}{PB}$=$\frac{2}{3}$,∴DM∥AE,
∵DM?面AEF,AE?面AEF,
∴DM∥平面AEF,
∵E,F分别是PD,PC的中点,
∴CD∥EF,CD?面AEF,EF?平面AEF,
∴CD∥平面AEF,CD∩DM=D,CD?面CDM,DM?面CDM,
∴面CDM∥面AEF,
∵CM?面CDM,∴CM∥面AEF.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,考查线满足线面平行的点的确定与求法,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
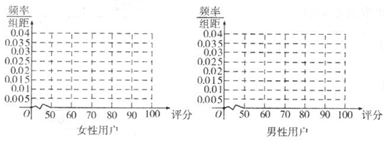
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,再从这20名用户中满足评分不低于80分的用户中任意抽取2名用户,求2名用户评分都小于90分的概率.
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | {-3,-2} | B. | {2,3} | C. | (-3,-2) | D. | (2,3) |
| 组号 | 分组 | 频数 |
| 1 | [0.5,1) | 20 |
| 2 | [1,1.5) | 40 |
| 3 | [1.5,2) | 80 |
| 4 | [2,2.5) | 120 |
| 5 | [2.5,3) | 60 |
| 6 | [3,3.5) | 40 |
| 7 | [3.5,4) | 20 |
| 8 | [4,4.5) | 20 |
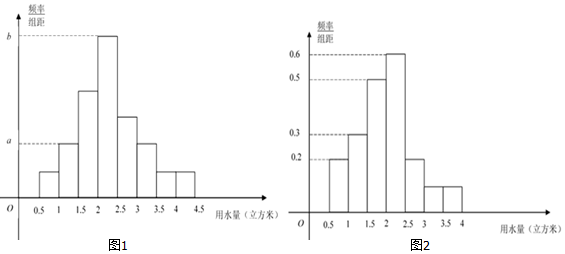
(Ⅱ)从该小区随机选取一名住户,试估计这名住户一个月用水量小于3立方米的概率;
(Ⅲ)若小区人均月用水量低于某一标准,则称该小区为“节水小区”.假设同组中的每个数据用该组区间的右端点值代替,经过估算,该小区未达到“节水小区”标准,而且该小区居民月用水量不高于这一标准的比例为65%,经过同学们的节水宣传,三个月后,又进行一次同等规模的随机抽样调查,数据如图2所示,估计这时小区是否达到“节水小区”的标准?并说明理由.
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∨(¬q) | D. | (¬p)∧(¬q) |
| A. | 仅有极小值的奇函数 | B. | 仅有极小值的偶函数 | ||
| C. | 仅有极大值的偶函数 | D. | 既有极小值也有极大值的奇函数 |