题目内容
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元.
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)设该厂的月获利为y,则y=(160-2x)x-(500+30x)=-2x2+130x-500,解不等式-2x2+130x-500≥1300;
(2)由(1)知,利用配方法求y=-2x2+130x-500=-2(x-
)2+1612.5的最大值及最大值点.
(2)由(1)知,利用配方法求y=-2x2+130x-500=-2(x-
| 65 |
| 2 |
解答:
解:(1)设该厂的月获利为y,由题意得,
y=(160-2x)x-(500+30x)=-2x2+130x-500,
由y≥1300得,
-2x2+130x-500≥1300,
∴x2-65x+900≤0,
∴(x-20)(x-45)≤0,解得20≤x≤45;
∴当月产量在20~45件之间时,月获利不少于1300元.
(2)由(1)知y=-2x2+130x-500=-2(x-
)2+1612.5
∵x为正整数,
∴x=32或33时,
y取得最大值为1612元,
∴当月产量为32件或33件时,可获得最大利润1612元.
y=(160-2x)x-(500+30x)=-2x2+130x-500,
由y≥1300得,
-2x2+130x-500≥1300,
∴x2-65x+900≤0,
∴(x-20)(x-45)≤0,解得20≤x≤45;
∴当月产量在20~45件之间时,月获利不少于1300元.
(2)由(1)知y=-2x2+130x-500=-2(x-
| 65 |
| 2 |
∵x为正整数,
∴x=32或33时,
y取得最大值为1612元,
∴当月产量为32件或33件时,可获得最大利润1612元.
点评:本题考查了学生将实际问题转化为数学问题的能力,同时考查了配方法求函数的最值,属于中档题.

练习册系列答案
相关题目
已知a,b均为单位向量,其夹角为θ,有下列四个命题
p1:|a+b|>1?θ∈[0,
)
p2:|a+b|>1?θ∈(
,π]
p3:|a-b|>1?θ∈[0,
)
p4:|a-b|>1?θ∈(
,π]
其中真命题是( )
p1:|a+b|>1?θ∈[0,
| 2π |
| 3 |
p2:|a+b|>1?θ∈(
| 2π |
| 3 |
p3:|a-b|>1?θ∈[0,
| π |
| 3 |
p4:|a-b|>1?θ∈(
| π |
| 3 |
其中真命题是( )
| A、p1,p4 |
| B、p1,p3 |
| C、p2,p3 |
| D、p2,p4 |
数列{an}满足a1=3,an-anan+1=1,An表示{an}的前n项之积,则A2009等于( )
| A、2 | B、-2 | C、3 | D、-3 |
已知P是△ABC所在平面内一点,且|
|2+|
|2=|
|2+|
|2,则( )
| PA |
| BC |
| PB |
| CA |
| A、PC⊥AB |
| B、PC平分∠ACB |
| C、PC过AB的中点 |
| D、P是△ABC的外心 |
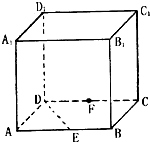 正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.
正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.