题目内容
如图,三棱柱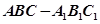 中,
中,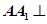 平面
平面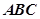 ,
,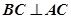 ,
,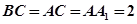 ,
,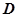 为
为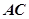 的中点.
的中点.

(1)求证: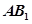 ∥平面
∥平面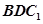 ;
;
(2)求二面角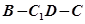 的余弦值;
的余弦值;
(3)设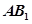 的中点为
的中点为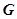 ,问:在矩形
,问:在矩形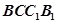 内是否存在点
内是否存在点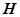 ,使得
,使得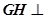 平面
平面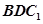 .若存在,求出点
.若存在,求出点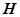 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
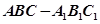 中,
中,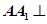 平面
平面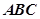 ,
,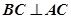 ,
,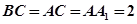 ,
,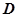 为
为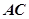 的中点.
的中点.
(1)求证:
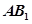 ∥平面
∥平面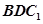 ;
;(2)求二面角
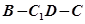 的余弦值;
的余弦值;(3)设
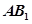 的中点为
的中点为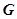 ,问:在矩形
,问:在矩形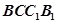 内是否存在点
内是否存在点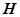 ,使得
,使得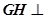 平面
平面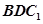 .若存在,求出点
.若存在,求出点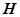 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.(1) 只需证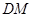 ∥
∥ ;(2)
;(2)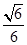 ;(3)
;(3)
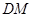 ∥
∥ ;(2)
;(2)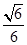 ;(3)
;(3)试题分析:(1)连结
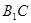 ,设
,设 ,连结
,连结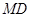 ,在
,在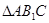 中,
中, 为
为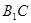 中点,
中点,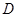 为
为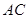 中点,∴
中点,∴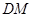 ∥
∥ ,又∵
,又∵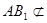 面
面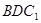 ,
, 面
面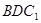 ,
,∴
 ∥面
∥面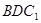 . 4分
. 4分(2)过
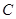 作
作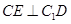 且设
且设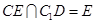 ,连结
,连结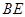 ,∵
,∵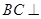 面
面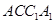 ,
,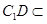 面
面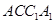 ,∴
,∴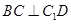 .又
.又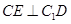 ,∴
,∴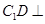 面
面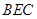 ,∴
,∴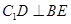 ,∴
,∴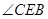 为二面角
为二面角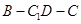 的平面角,设为
的平面角,设为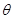 . 5分
. 5分在
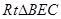 中,
中,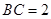 ,由
,由 可得
可得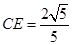 ,
,∴
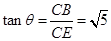 ,即二面角
,即二面角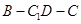 的余弦值为
的余弦值为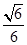 . 8分
. 8分(3)以
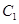 为坐标原点,
为坐标原点,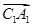 为
为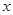 轴,
轴,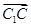 为
为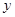 轴,
轴,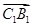 为
为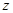 轴建立空间直角坐标系.
轴建立空间直角坐标系.依题意,得:
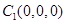 、
、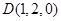 、
、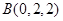 、
、 ,假设存在
,假设存在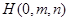
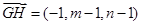 ,
,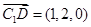 ,
,
由
 平面
平面 ,得:
,得:
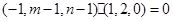 ∴
∴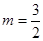
同理,由
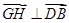 得:
得: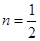
即:在矩形
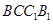 内是存在点
内是存在点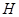 ,使得
,使得 平面
平面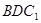 .此时点
.此时点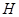 到
到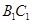 的距离为
的距离为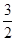 ,到
,到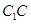 的距离为
的距离为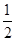 . 13分
. 13分 点评:立体几何中证明线面平行或面面平行都可转化为“线线平行”,而证明线线平行一般有以下的一些方法: (1) 通过“平移”。 (2) 利用三角形中位线的性质。 (3) 利用平行四边形的性质。 (4) 利用对应线段成比例。 (5) 利用面面平行,等等。

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。
 ;
; 与平面
与平面 所成的角的大小;
所成的角的大小; 的正切值。
的正切值。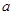 的菱形
的菱形 中,
中,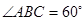 ,
,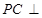 面
面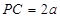 ,
,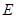 、
、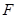 分别是
分别是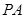 和
和 的中点.
的中点.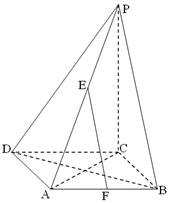
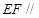 面
面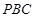 ;
; 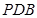 ⊥平面
⊥平面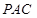 ;
;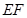 与平面
与平面 中,底面
中,底面 是正方形,侧面
是正方形,侧面 是正三角形,且平面
是正三角形,且平面
 ⊥平面
⊥平面 与底面
与底面 ,求点
,求点 到平面
到平面 的距离.
的距离.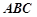 是正三角形,
是正三角形,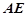 和
和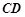 都垂直于平面
都垂直于平面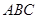 ,且
,且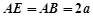 ,
,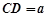 ,
,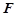 是
是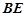 的中点.
的中点.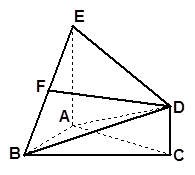
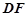 ∥平面
∥平面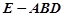 的体积.
的体积. ,
, ,
, ,
,

 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由. 中,下面结论错误的是( )
中,下面结论错误的是( )


 所成角为450
所成角为450 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有下列命题:
,有下列命题: ∥
∥
 ∥m;
∥m;