题目内容
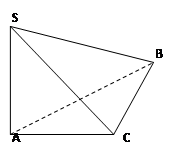
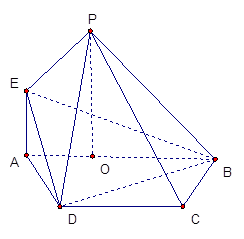
如图:在三棱锥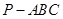 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。

⑴求证: ;
;
⑵求直线 与平面
与平面 所成的角的大小;
所成的角的大小;
⑶求二面角 的正切值。
的正切值。
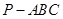 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。
⑴求证:
 ;
;⑵求直线
 与平面
与平面 所成的角的大小;
所成的角的大小;⑶求二面角
 的正切值。
的正切值。(1)见解析 (2) (3)
(3)
 (3)
(3)
【错解分析】立体几何是高考的必考内容,容易错误的地方通常是求二面角的大小,因此要归纳总结通常寻找二面角的平面角的方法。
【正解】⑴连结
 。在
。在 中,
中,

 ,点
,点 为
为 的中点,
的中点,

又

 面
面 ,即
,即 为
为 在平面
在平面 内的射影
内的射影


 分别为
分别为 的中点
的中点



⑵

 面
面 ,
,

连结
 交
交 于点
于点 ,
,
 ,
,
 平面
平面

 为直线
为直线 与平面
与平面 所成的角,且
所成的角,且

 面
面 ,
,
 ,又
,又


 ,
,
 ,
,

 在
在 中,
中, ,
,

⑶过点
 作
作 于点
于点 ,连结
,连结 ,
,
 ,
,
 面
面 ,即
,即 为
为 在平面
在平面 内的射影
内的射影
 ,
,
 为二面角
为二面角 的平面角
的平面角 
 中,
中, ,
,


练习册系列答案
相关题目
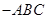 中
中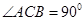 ,
,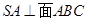 ,
,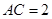 ,
,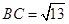 ,
,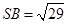 .
.
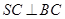 。
。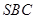 与底面
与底面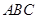 所成二面角的大小。
所成二面角的大小。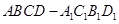 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱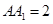 ,为
,为 中点,
中点,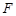 为
为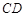 中点,
中点,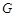 为
为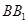 上一个动点.
上一个动点.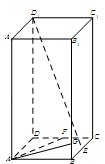
 ;
;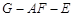 的平
的平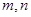 相交,且
相交,且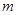 ∥平面
∥平面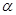 ,则
,则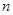 与
与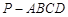 的底面
的底面 为菱形,
为菱形,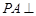 平面
平面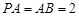 , E、F分别为
, E、F分别为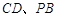 的中点,
的中点,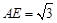 .
.
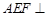 平面
平面 .
. 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.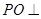 平面
平面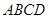 ,点
,点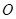 在
在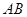 上,
上,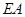 ∥
∥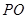 ,四边形
,四边形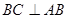 ,
,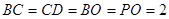 ,
,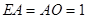
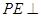 平面
平面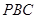 ;
;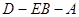 的余弦值;
的余弦值;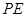 上是否存在点
上是否存在点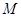 ,使
,使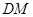 ∥平面
∥平面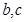 表示两条直线,
表示两条直线,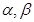 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( ) ,
, ∥
∥ ,则
,则

 ,则
,则

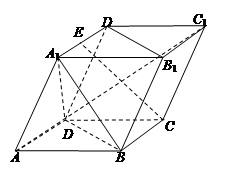
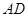 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④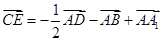 ;⑤|
;⑤|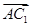 |=
|=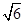 .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)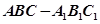 中,
中,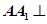 平面
平面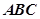 ,
,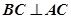 ,
,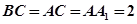 ,
,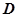 为
为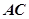 的中点.
的中点.
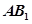 ∥平面
∥平面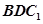 ;
;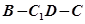 的余弦值;
的余弦值;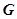 ,问:在矩形
,问:在矩形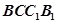 内是否存在点
内是否存在点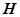 ,使得
,使得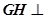 平面
平面