题目内容
如图,在五面体ABCDEF中, ,
, ,
, ,
,

(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.
 ,
, ,
, ,
,

(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为
 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.(Ⅰ)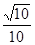 ;(Ⅱ)存在,点M为CE中点。
;(Ⅱ)存在,点M为CE中点。
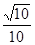 ;(Ⅱ)存在,点M为CE中点。
;(Ⅱ)存在,点M为CE中点。试题分析:解法一:建立如图所示的直角坐标系, ……2分
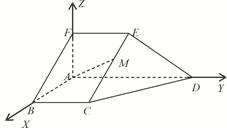
不妨设AB=1
则
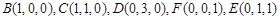
(Ⅰ)
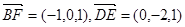
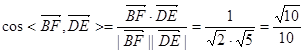 ……5分
……5分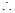 异面直线BF与DE所成角的余弦值为
异面直线BF与DE所成角的余弦值为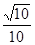 . ……6分
. ……6分(Ⅱ)设平面CDE的一个法向量为
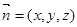
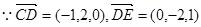
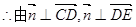 得
得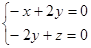 令
令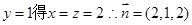 ……8分
……8分设存在点M
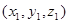 满足条件,由
满足条件,由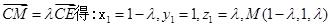
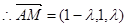 ……10分
……10分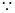 直线AM与平面CDE所成角的正弦值为
直线AM与平面CDE所成角的正弦值为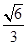
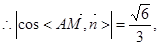
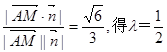
故当点M为CE中点时,直线AM与面CDE所成角的正弦值为
 . ……13分
. ……13分解法二:(Ⅰ)不妨设AB=1,
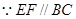 且
且
∴∠CED异面直线BF与DE所成角
CE=BF=
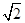 ,ED=DC=
,ED=DC=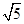 ,
,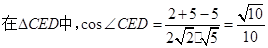
所以,异面直线BF与DE所成角的余弦值为
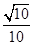 ……6分
……6分(Ⅱ)令A到平面CDE距离为h,在AD上取点N,使得EF=AN,连结EN
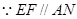 ,
,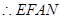 为平行四边形
为平行四边形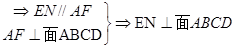 ……8分
……8分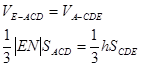
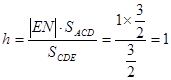 ……10分
……10分令AM与平面CDE所成角为
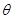 ,
,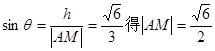
过M作MG//EF交FB于G
在平行四边形EFBC中,MG=BC=1
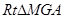 中
中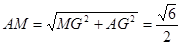
解得:
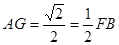 ,
,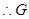 为FB的中点
为FB的中点 MG//EF,
MG//EF, 为EC的中点。 ……13分
为EC的中点。 ……13分点评:从近些年看,以多面体为载体,重点考查直线与平面的位置关系一直是高考立体几何命题的热点.因为这类题目既可以考查多面体的概念和性质,又能考查空间的线面关系,并将论证和计算有机地结合在一起

练习册系列答案
相关题目
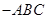 中
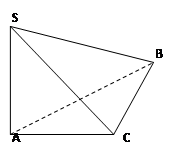
中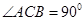 ,
,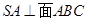 ,
,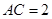 ,
,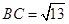 ,
,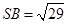 .
.
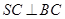 。
。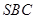 与底面
与底面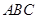 所成二面角的大小。
所成二面角的大小。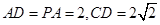 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点.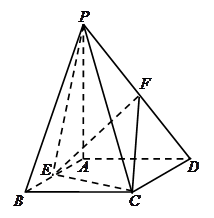
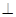 平面PCD;
平面PCD; 中,
中,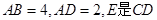 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且 .
.

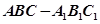 中,
中,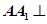 平面
平面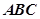 ,
,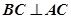 ,
,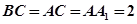 ,
,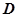 为
为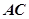 的中点.
的中点.
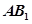 ∥平面
∥平面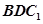 ;
;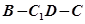 的余弦值;
的余弦值;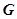 ,问:在矩形
,问:在矩形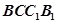 内是否存在点
内是否存在点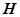 ,使得
,使得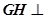 平面
平面 平面ABCD,
平面ABCD, ,BC=1,E为CD的中点,PC与平面ABCD成
,BC=1,E为CD的中点,PC与平面ABCD成 角。
角。
 中,底面
中,底面 为正方形,
为正方形, 平面
平面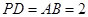 ,
, ,
, ,
, 分别为
分别为 、
、 、
、 的中点.
的中点.
 ;
; 、
、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则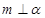
 ,
, ,则
,则