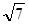题目内容
已知直线 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有下列命题:
,有下列命题:
① ∥
∥

 ⊥m; ②
⊥m; ② ⊥
⊥

 ∥m;
∥m;
③ ∥m
∥m
 ⊥
⊥ ; ④
; ④ ⊥m
⊥m
 ∥
∥ .
.
其中正确命题的序号是 。
 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有下列命题:
,有下列命题:①
 ∥
∥

 ⊥m; ②
⊥m; ② ⊥
⊥

 ∥m;
∥m;③
 ∥m
∥m
 ⊥
⊥ ; ④
; ④ ⊥m
⊥m
 ∥
∥ .
.其中正确命题的序号是 。
①与③
试题分析:①因为直线
 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,
, ∥
∥ ,所以
,所以 ⊥平面
⊥平面 ,从而
,从而 ⊥m,正确;②因为直线
⊥m,正确;②因为直线 ⊥平面
⊥平面 ,
, ⊥
⊥ ,所以
,所以 ∥
∥ 或
或
 ,而m
,而m 平面
平面 ,所以l,m的关系有平行,相交等可能,此不正确;
,所以l,m的关系有平行,相交等可能,此不正确;点评:基础题,注意线线,线面,面面平行关系及垂直关系的转化.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
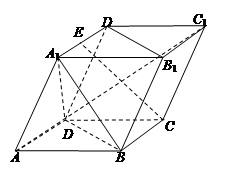
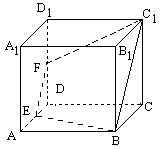
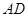 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④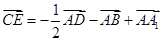 ;⑤|
;⑤|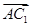 |=
|=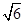 .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)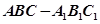 中,
中,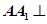 平面
平面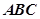 ,
,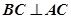 ,
,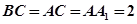 ,
,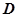 为
为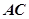 的中点.
的中点.
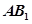 ∥平面
∥平面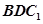 ;
;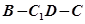 的余弦值;
的余弦值;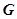 ,问:在矩形
,问:在矩形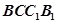 内是否存在点
内是否存在点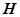 ,使得
,使得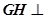 平面
平面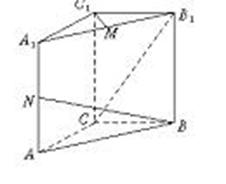
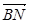 的长; (2)求cos<
的长; (2)求cos<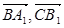 >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.  中,底面
中,底面 为正方形,
为正方形, 平面
平面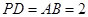 ,
, ,
, ,
, 分别为
分别为 、
、 、
、 的中点.
的中点.
 ;
;
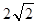 B.
B. 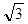 C.
C. 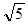 D.
D.