题目内容
18. 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.(1)求证:AO⊥CF;
(2)求O到平面ABC的距离.
分析 (1)证明AO⊥EF,推出AO⊥平面EFCB,即可证明AO⊥CF.
(2)取BC的中点G,连接OG.推出OG⊥BC,OA⊥BC,得到BC⊥平面AOG,过O作OH⊥AG,垂足为H,说明OH⊥平面ABC,O到平面ABC的距离为OH,求解即可.
解答 (1)证明:因为△AEF等边三角形,O为EF的中点,所以AO⊥EF…(1分)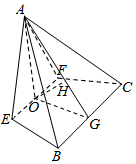
又因为平面AEF⊥平面EFCB,AO?平面AEF,平面AEF∩平面EFCB=EF,
所以AO⊥平面EFCB,…(4分)
又CF?平面EFCB,所以AO⊥CF…(5分)
(2)解:取BC的中点G,连接OG.
由题设知,OG⊥BC…(6分)
由(1)知AO⊥平面EFCB,
又BC?平面EFCB,所以OA⊥BC,因为OG∩OA=O,所以BC⊥平面AOG…(8分)
过O作OH⊥AG,垂足为H,则BC⊥OH,因为AG∩BC=G,所以OH⊥平面ABC.
…(10分)
因为$OG=\sqrt{3},AO=\sqrt{3}$,所以$OH=\frac{{\sqrt{6}}}{2}$,
即O到平面ABC的距离为$\frac{{\sqrt{6}}}{2}$.(另外用等体积法亦可)…(12分)
点评 本题考查直线与平面垂直的判定定理的应用,空间点、线、面距离的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
10.已知函数y=f(x-2)-1是奇函数,则函数y=f(x)的图象关于( )
| A. | 直线x=-2对称 | B. | 直线x=2对称 | C. | 点(2,-1)对称 | D. | 点(-2,1)对称 |
6.已知离散型随机变量X的分布列如表:若E(X)=0,D(X)=1,则P(X<1)等于( )
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{1}{12}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
13.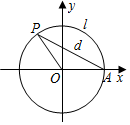 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π| A. | 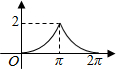 | B. | 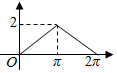 | C. |  | D. | 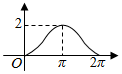 |
7.下列命题中正确的是( )
| A. | 若ξ服从正态分布N(0,2),且P(ξ>2)=0.4,则P(0<ξ<2)=0.2 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |