题目内容
18.设函数f(x)=x2+mln(x+1).(1)若m=-1,试比较当x∈(0,+∞)时,f(x)与x3的大小;
(2)证明:对任意的正整数n,不等式e0+e-1×4+e-2×9+…${e}^{(1-n){n}^{2}}$<$\frac{n(n+3)}{2}$恒成立.
分析 (1)令g(x)=f(x)-x3,求导判断g(x)的单调性和最大值;
(2)由(1)可知x2-x3<ln(x+1)(x>0),变形为e(1-x)x2<x+1,累加计算即可.
解答 解:(1)m=-1时,f(x)=x2-ln(x+1).
令g(x)=f(x)-x3=x2-x3-ln(x+1).
∴g′(x)=2x-3x2-$\frac{1}{x+1}$=-$\frac{3{x}^{3}+(x-1)^{2}}{x+1}$.
∵x∈(0,+∞),∴g′(x)<0.
∴g(x)在(0,+∞)上是减函数.∴g(x)<g(0)=0.
∴f(x)-x3<0,即f(x)<x3.
(2)由(1)可知x2-x3<ln(x+1),(x>0).
∴e${\;}^{{x}^{2}-{x}^{3}}$<x+1.即e${\;}^{{x}^{2}(1-x)}$<x+1.(x>0).
∴e${\;}^{{n}^{2}(1-n)}$<n+1.(n∈N+).
∴e0+e-1×4+e-2×9+…${e}^{(1-n){n}^{2}}$<(1+1)+(2+1)+(3+1)+…+(n+1)=(1+2+3…+n)+n
$\frac{(1+n)n}{2}+n$=$\frac{n(n+3)}{2}$.
点评 本题考查利用导数研究函数的单调性,以及函数单调区间等有关基础知识,应用导数研究函数单调性的方法及推理和运算能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.执行如图的程序框图,如果输入的N=100,则输出的x=( )
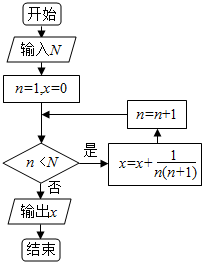

| A. | 0.95 | B. | 0.98 | C. | 0.99 | D. | 1.00 |
10.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则sin(2α-β)+sin(α-2β)的取值范围为( )
| A. | [-$\sqrt{2}$,1] | B. | [-1,$\sqrt{2}$] | C. | [-1,1] | D. | [1,$\sqrt{2}$] |