题目内容
3.在△ABC中,角A,B,C的对边分别为a,b,c,已知cos(B-C)=1-cosA,且b,a,c成等比数列,求:(1)sinB•sinC的值;
(2)A;
(3)tanB+tanC的值.
分析 (1)利用三角形内角和定理及两角和的余弦函数公式化简cos(B-C)=1-cosA即可求得sinBsinC的值.
(2)由等比数列的性质可得a2=bc,由正弦定理得sin2A=sinBsinC,由(1)解得sin2A=$\frac{1}{2}$,结合范围A∈(0,π),a边不是最大边,即可解得A的值.
(3)由B+C=π-A=$\frac{3π}{4}$,可得cos(B+C)=cosBcosC-sinBsinC=-$\frac{\sqrt{2}}{2}$,解得cosBcosC的值,利用同角三角函数基本关系式及两角和的正弦函数公式化简所求后计算即可得解.
解答 (本题满分为14分)
解:(1)∵cos(B-C)=1-cosA=1+cos(B+C),
∴cosBcosC+sinBsinC=1+cosBcosC-sinBsinC,
∴sinBsinC=$\frac{1}{2}$.…2分
(2)∵b,a,c成等比数列,∴a2=bc,
由正弦定理,可得sin2A=sinBsinC,
从而sin2A=$\frac{1}{2}$,
因为A∈(0,π),所以sinA=$\frac{\sqrt{2}}{2}$,
又因为a边不是最大边,所以A=$\frac{π}{4}$…8分
(3)因为B+C=π-A=$\frac{3π}{4}$,
所以cos(B+C)=cosBcosC-sinBsinC=-$\frac{\sqrt{2}}{2}$,
从而cosBcosC=$\frac{1-\sqrt{2}}{2}$,…10分
所以tanB+tanC=$\frac{sinB}{cosB}+\frac{sinC}{cosC}$=$\frac{sin(B+C)}{cosBcosC}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1-\sqrt{2}}{2}}$=-2-$\sqrt{2}$…14分
点评 本题主要考查了三角形内角和定理及两角和的余弦函数公式,等比数列的性质,正弦定理,同角三角函数基本关系式及两角和的正弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

| A. | y2=-x | B. | x2=y | C. | y2=-x或x2=y | D. | y2=x或x2=-y |
| A. | 60、50、40 | B. | 50、60、40 | C. | 40、50、60 | D. | 60、40、50 |
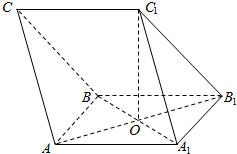 如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.
如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.