题目内容
m=1是直线2mx+4y+16=0和直线x+(1+m)y+m-2=0平行的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据直线平行的等价条件,结合充分条件和必要条件的定义进行判断.
解答:
解:若m=0,则两直线等价为y=-4和x+y-2=0,此时两直线不平行,
∴m≠0,
若直线平行,则满足
=
≠
,
由
=
得m2+m-2=0,解得m=1或m=-2,
由
≠
得m≠-2,
综上m=1,
∴m=1是直线2mx+4y+16=0和直线x+(1+m)y+m-2=0平行充要条件,
故选:C
∴m≠0,
若直线平行,则满足
| 1 |
| 2m |
| 1+m |
| 4 |
| m-2 |
| 16 |
由
| 1 |
| 2m |
| 1+m |
| 4 |
由
| 1+m |
| 4 |
| m-2 |
| 16 |
综上m=1,
∴m=1是直线2mx+4y+16=0和直线x+(1+m)y+m-2=0平行充要条件,
故选:C
点评:本题主要考查充分条件和必要条件的判断,根据直线平行的等价条件求出m是解决本题的关键.

练习册系列答案
相关题目
已知两个向量
=(t,
),
=(x+1,
),其中t,u都是正实数,且
=2
,则
的取值范围是( )
| a |
| x |
| b |
| u |
| 2 |
| a |
| b |
| t |
| u |
| A、[1,6] |
| B、[-6,1] |
| C、[4,+∞) |
| D、(-∞,1] |
设a,b∈R,则“a+b>4”是“a>2,且b>2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
函数y=lg(x-5)的定义域为M,函数y=lg(x-5)+lg(12-x)的定义域为N,则( )
| A、M∪N=R | B、M=N |
| C、M?N | D、M⊆N |
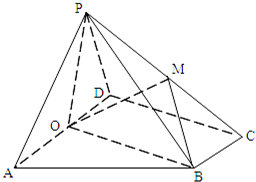 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.