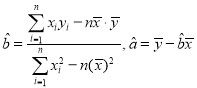题目内容
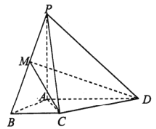
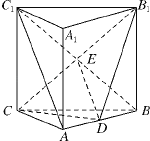
【题目】如图所示,在直三棱柱![]() 中,D点为棱AB的中点.
中,D点为棱AB的中点.

![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 若
若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值;
的余弦值;
![]() 若
若![]() ,
,![]() ,
,![]() 两两垂直,求证:此三棱柱为正三棱柱.
两两垂直,求证:此三棱柱为正三棱柱.
【答案】(1)见解析
(2)![]()
(3)见解析
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 是△
是△![]() 的中位线,所以
的中位线,所以![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() 为二面角
为二面角![]() 的平面角;
的平面角;
(3)作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() 是等边三角形,又三棱柱
是等边三角形,又三棱柱![]() 是直三棱柱,即可证明结论.
是直三棱柱,即可证明结论.
(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 是△
是△![]() 的中位线,所以
的中位线,所以![]()
又 ![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() .
.
(2)解:过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 为二面角
为二面角![]() 的平面角,设
的平面角,设![]()
由已知可得![]() ,
,![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.

(3)证明:作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
由已知可得 ![]() 平面
平面![]() ,
,![]()
又 ![]() ,且
,且![]() ,
,![]() 是平面
是平面![]() 内的两条相交直线,
内的两条相交直线,
![]() 平面
平面![]() ,
,![]()
同理 ![]()
又 直线![]() ,
,![]() ,
,![]() 都在平面
都在平面![]() 内,
内,![]() ,
,
又![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]()
又△![]() ,
,![]() ,
,![]()
同理![]() ,
,
![]() 是等边三角形,又三棱柱
是等边三角形,又三棱柱![]() 是直三棱柱
是直三棱柱![]() 三棱柱
三棱柱![]() 为正三棱柱.
为正三棱柱.


练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: