题目内容
【题目】若函数![]() 在其定义域上恰有两个零点,则正实数a的值为_____.
在其定义域上恰有两个零点,则正实数a的值为_____.
【答案】![]()
【解析】
当x≤0时,f(x)=x+2x,单调递增,由f(﹣1)f(0)<0,可得f(x)在(﹣1,0)有且只有一个零点;x>0时,f(x)=ax﹣lnx有且只有一个零点,即有a![]() 有且只有一个实根.令g(x)
有且只有一个实根.令g(x)![]() ,求出导数,求得单调区间,极值,即可得到a的值.
,求出导数,求得单调区间,极值,即可得到a的值.
当x≤0时,f(x)=x+2x,单调递增,
f(﹣1)=﹣1+2﹣1<0,f(0)=1>0,
由零点存在定理,可得f(x)在(﹣1,0)有且只有一个零点;
则由题意可得x>0时,f(x)=ax﹣lnx有且只有一个零点,
即有a![]() 有且只有一个实根.
有且只有一个实根.
令g(x)![]() ,g′(x)
,g′(x)![]() ,
,
当x>e时,g′(x)<0,g(x)递减;
当0<x<e时,g′(x)>0,g(x)递增.
即有x=e处取得极大值,也为最大值,且为![]() ,当x
,当x![]()
如图g(x)的图象,当直线y=a(a>0)与g(x)的图象
只有一个交点时,则a![]() .
.
故答案为:![]() .
.


练习册系列答案
相关题目
【题目】某企业为了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 的数据作了初步整理,得到下面的表格:
的数据作了初步整理,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
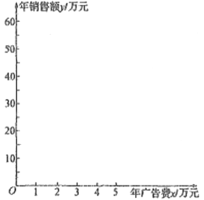
(1)用年广告费![]() 作解释变量,年销售额
作解释变量,年销售额![]() 作预报变量,在所给坐标系中作出这些数据的散点图,并判断
作预报变量,在所给坐标系中作出这些数据的散点图,并判断![]() 与
与![]() 哪一个更适合作为年销售额
哪一个更适合作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型(给出判断即可,不必说明理由).
的回归方程类型(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() .根据(2)的结果,计算年广告费
.根据(2)的结果,计算年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据
约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为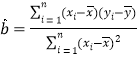 ,
,![]() .
.